Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Curvas Polares

Ver Todos os Exercícios

Teoria

Introdução

Neste tópico nós vamos aprender a determinar a área delimitada de algumas curvas!

Então vamos com um exemplo: como determinar a área delimitada pela curva abaixo?

x 2 + y 2 2 = 2 x 2 - y 2

Calma! Vamos passo a passo.

Repara que nós temos os termos x 2   e   y 2 . Quando a gente tiver esses termos elevado ao quadrado, a dica é usar coordenadas polares. Então ficará assim,

x = r cos ⁡ θ

y = r   s e n   θ

J = r

Se introduzirmos essa mudança na expressão da curva, temos

x 2 + y 2 2 = 2 x 2 - y 2

r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ 2 = 2 r 2 cos 2 ⁡ θ - r 2 sen 2 ⁡ θ

r 2 . cos 2 ⁡ θ + s e n 2 θ 2 = 2 ( r 2 . cos 2 ⁡ θ - s e n 2 θ )

Usando a propriedade cos 2 ⁡ θ + s e n 2 θ = 1 e cos 2 ⁡ θ - sen 2 ⁡ θ = cos ⁡ 2 θ , temos

r 4 = 2 r 2 cos ⁡ 2 θ → r 2 = 2 cos ⁡ 2 θ ∴ r = 2 cos ⁡ 2 θ

Nós chamamos de curvas polares, todas essas curvas nas quais podemos aplicar as coordenadas polares. Elas, normalmente, são difíceis de serem desenhadas, então fica difícil de achar a variação do ângulo θ .

Por isso, vou te contar o segredo por trás do truque de mágica, a gente sempre pode considerar essa variação aqui:

r ≥ 0   e   θ i ≤ θ ≤ θ i + 2 π

Onde θ i é o ângulo inicial. A gente aqui vai adotar que θ i = 0 para todos os casos. Dessa forma, só poderemos ter valores de θ entre 0 e 2 π . Não entendeu nada? Vamos seguir com o exemplo,

Temos que r = 2 cos ⁡ 2 θ e r ≥ 0 , então,

2 cos ⁡ 2 θ ≥ 0 → cos ⁡ 2 θ ≥ 0 ∴ - π 2 ≤ 2 θ ≤ π 2

Se lembrarmos lá do círculo trigonométrico a gente vai concluir que existem mais intervalos que são válidos como, por exemplo:

3 π 2 ≤ 2 θ ≤ 5 π 2

7 π 2 ≤ 2 θ ≤ 9 π 2

⋮

Ok, mas devemos analisar θ e não 2 θ . Então devemos dividir todo mundo por 2. Assim, os ângulos que satisfazem a primeira condição são

- π 4 ≤ θ ≤ π 4

3 π 4 ≤ θ ≤ 5 π 4

7 π 4 ≤ θ ≤ 9 π 4 ,

⋮

Agora, lembra da segunda condição? Devemos garantir que, no máximo, 0 ≤ θ ≤ 2 π . Vemos, então, que os únicos ângulos que satisfazem as duas condições, ao mesmo tempo, são

0 ≤ θ ≤ π 4 , 3 π 4 ≤ θ ≤ 5 π 4 , 7 π 4 ≤ θ ≤ 2 π

Estamos acabando, acredite em mim! A variação de θ é dado pelos intervalos acima e a variação de r é 0 ≤ r ≤ 2 cos ⁡ 2 θ . Então, já estamos aptos a montar as integrais. Lembrando que a integral aplicando mudança de coordenadas polares tem a seguinte cara,

A = ∬ f r , θ | J | d r d θ

Mas para cada intervalo de θ , nós vamos ter uma integral e vamos precisar do somatório delas.

A = ∫ 0 π / 4 ∫ 0 2 cos ⁡ 2 θ r d r d θ + ∫ 3 π / 4 5 π / 4 ∫ 0 2 cos ⁡ 2 θ r d r d θ + ∫ 7 π / 4 2 π ∫ 0 2 cos ⁡ 2 θ r d r d θ

Agora é só resolver essas integrais e somar o resultado. Quer ver qual é essa figura? Olha um esboço dela aqui:

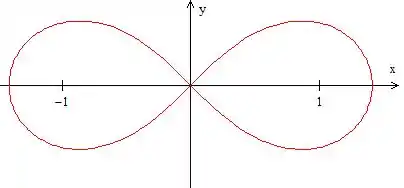
Curvas Polares na forma parametrizada

Galera, se liga em outra coisa agora! Muitas vezes a questão te dá curva parametrizada. Então como a gente faz?

Olha esse exemplo e temos quer calcular a área limitada por ele:

c θ = 1 + cos ⁡ θ cos ⁡ θ , 1 + cos ⁡ θ ) sen ⁡ θ                                 ( 1 )

O macetinho aqui é comparar essa expressão de cima ( 1 ) com essa aqui embaixo ( 2 )

c θ = r θ cos ⁡ θ ,   r θ sen ⁡ θ                               ( 2 )

Repara só que r θ da expressão ( 2 ) equivale ao 1 + cos ⁡ θ da expressão ( 1 ) . Como vimos acima r ≥ 0 . Deste modo,

r θ = 1 + cos ⁡ θ ≥ 0

cos ⁡ θ ≥ - 1

Agora, acharemos a variação de θ . Como qualquer ângulo pode satisfazer essa condição teríamos

- ∞ ≤ θ ≤ ∞

Mas, pela segunda condição vamos ter, na verdade,

0 ≤ θ ≤ 2 π

Então, jogando novamente na formula de mudanças de coordenadas polares, a área pedida pode ser calculada com

A = ∫ 0 2 π ∫ 0 1 + cos ⁡ θ r d r d θ  

Vamos escrever um passo a passo então?

Passo 1: escrever a mudança polar ou elíptica e não esquecer do jacobiano.

Passo 2: introduzir a mudança na equação da curva que foi dada e obter o valor de r máximo.

Passo 3: usar as hipóteses r ≥ 0 e 0 ≤ θ ≤ 2 π para achar a real variação de θ .

Passo 4: escrever os limites de integração.

Passo 5: montar e resolver as integrais

Agora partiu exercícios. That’s all Folks.

Curvas Polares na forma parametrizada

Exercícios Resolvidos

Exercício Resolvido #1

CEFET - Cálculo 2 - P2 Pericles 2014.2 – 4

Ache a massa da lâmina na forma da região exterior à limaçon r = 3 - cos ⁡ θ e interior à circunferência r = 5 cos ⁡ θ , se a densidade de massa por unidade de àrea em qualquer ponto for 2 s e n   θ k g / m 2 .

Passo 1

Vamos começar fazendo um desenho dessa região para entender melhor o que está acontecendo.

O esboço das regiões é esse aqui em baixo: Mas na prática você não precisa saber desenhar isso (ninguém sabe desenhar uma limaçon haha)

O que o problema pede é então o seguinte:

M = ∬ D   ρ x , y d x d y

Onde D é a região em cinza que vimos na figura.

Passo 2

Agora precisamos descrever a região. E como o problema já nos dá as equações em coordenadas polares, vamos usar coordenadas polares né.

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Já temos a função densidade de área em coordenadas polares também, então a integral fica o seguinte:

M = ∬ R   2 s e n   θ r d r d θ

Pela figura, vemos que r varia desde a equação da circunferência vermelha r = 3 - cos ⁡ θ até a da azul r = 5 cos ⁡ θ . Agora falta descobrir o intervalo de θ , para isso, vamos fazer a interseção entre as duas curvas:

r = 3 - cos ⁡ θ = 5 cos ⁡ θ

6 cos ⁡ θ = 3

cos ⁡ θ = 1 2

θ = ± π 3

Assim, sabemos que - π 3 ≤ θ ≤ π 3 e a integral fica:

M = 2 ∫ - π / 3 π / 3 ∫ 3 - cos ⁡ θ 5 cos ⁡ θ s e n   θ r d r d θ

Ou podemos escrever:

M = 4 ∫ 0 π / 3 ∫ 3 - cos ⁡ θ 5 cos ⁡ θ s e n   θ r d r d θ

Por causa da simetria da figura.

Passo 3

Agora vamos resolver essa integral ai, começando integrando em relação a r :

= 2 ∫ 0 π / 3 s e n   θ r 2 3 - cos ⁡ θ 5 cos ⁡ θ d θ =

= 2 ∫ 0 π / 3 s e n   θ ( 25 cos 2 ⁡ θ - 9 + 6 cos ⁡ θ - cos 2 ⁡ θ ) d θ =

= 2 ∫ 0 π / 3 s e n   θ ( 24 cos 2 ⁡ θ - 9 + 6 cos ⁡ θ ) d θ =

Como o seno é positivo para os valores de θ da integral, podemos retirar esse módulo sem problemas:

= 2 ∫ 0 π / 3 24 sin ⁡ θ cos 2 ⁡ θ - 9 sin ⁡ θ + 6 sin ⁡ θ cos ⁡ θ d θ =

Passo 4

Agora vamos integrar em relação a θ .

= 2 - 8 cos 3 ⁡ θ + 9 cos ⁡ θ - 3 cos 2 ⁡ θ 0 π / 3 =

= 2 - 8 8 + 9 2 - 3 4 + 8 - 9 + 3 =

= 9.5

Resposta

9.5

Exercício Resolvido #2

USP - Cálculo 3 - P1 - 2015 - 1a

Calcule a área de um laço da rosácea cuja equação em coordenadas polares é r θ = cos ⁡ 5 θ .

Passo 1

Bom, para você ter uma ideia, essa rosácea é assim:

Passo 2

Mas a questão pede a área de apenas um laço. Bom, tá na cara que é para usarmos coordenadas polares, né? O problema já deu a curva na forma polar.

Então vamos pensar nos intervalos. O de r é fácil, o raio varia desde a origem até a curva r = cos ⁡ 5 θ , logo, 0 ≤ r ≤ cos ⁡ 5 θ .

O de θ temos que pensar um poquinho. O que “define” uma pétala não é a curva passar pela origem. Digo, toda vez que ela vai e volta para a origem temos uma nova pétala. E a curva passa pela origem cada vez que o raio se anula, não é?

Então o intervalo de θ que marca uma pétala é aquele que faz r = 0 duas vezes.

r = cos ⁡ 5 θ = 0

5 θ = π 2 ; 3 π 2 …

Os dois primeiros valores de θ que fazem r = 0 são, portanto:

θ = π 10

θ = 3 π 10

Logo, π 10 ≤ θ ≤ 3 π 10 .

Passo 3

Agora vamos montar ai integral com o que encontramos:

A = ∫ D   d A = ∫ π 10 3 π 10 ∫ 0 cos ⁡ 5 θ r   d r d θ

Não se esqueça desse r do Jacobiano!

Passo 4

Agora vamos integrar isso ái

A = ∫ π 10 3 π 10 r 2 2 0 cos ⁡ 5 θ d θ

A = 1 2 ∫ π 10 3 π 10 cos 2 ⁡ 5 θ d θ

Agora precisamos usar essa identidade

cos 2 ⁡ t = 1 + cos ⁡ 2 t 2

Aplicando ao nosso problema, temos:

A = 1 2 ∫ π 10 3 π 10 1 + cos ⁡ 10 θ 2 d θ

A = 1 4 ∫ π 10 3 π 10 1 + cos ⁡ 10 θ d θ

A = 1 4 θ + 1 10 s e n 10 θ π 10 π 3 10 =

A = 1 4 2 π 10

A = π 20

Resposta

A = π 20

Exercício Resolvido #3

UFRJ - Cálculo 3 - P1 2015.1 - 1

Seja A ⊂ R 2 o conjunto limitado pela curva plana com parametrização dada por :

σ θ = 2 + s e n 4 θ cos ⁡ θ , 2 + s e n 4 θ sen ⁡ θ ,   θ ∈ 0,2 π

(veja figura 1). Determine a área de A .

Passo 1

Bom, a área de uma região plana A é dada por:

Á r e a = ∬ A   d x d y

Agora só precisamos escrever essa região A na integral.

Passo 2

Vamos usar coordenadaspolares por causa dessess senos e cossenos, ok?

Vamos pensar um pouquinho, as coordenadas polares nos dão que:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

Portanto, a parametrização de uma curva em coordenadas polares seria dada por:

σ θ = r cos ⁡ θ , r sen ⁡ θ

Onde r é constante ou função de θ , isso porque, como sabemos, uma curva deve ter um parâmetro! Então, na verdade é isso aqui:

σ θ = r ( θ ) cos ⁡ θ , r ( θ ) sen ⁡ θ

Comparando com a curva do problema

σ θ = 2 + s e n 4 θ cos ⁡ θ , 2 + s e n 4 θ sen ⁡ θ

Nós tiramos que

r θ = 2 + s e n 4 θ

Onde 0 ≤ θ ≤ 2 π . Percebeu?

Então, se a curva é dada, em coordenadas polares, por essa equação; Como podemos dizer que, para a área A , r varia desde a origem até a curva, temos:

0 ≤ r ≤ 2 + s e n 4 θ

Com

0 ≤ θ ≤ 2 π

O que nós acabamos de fazer foi descrever A em coordenadas polares.

Passo 3

Agora vamos fazer a mudança polar na integral:

A = ∫ D   d A = ∫ 0 2 π ∫ 0 2 + s e n 4 θ r   d r d θ

Não se esqueça desse r do Jacobiano!

Passo 4

Agora vamos integrar isso ái

A = ∫ 0 2 π r 2 2 0 2 + s e n 4 θ d θ

= 1 2 ∫ 0 2 π 4 + 4 s e n 4 θ + s e n 2 ( 4 θ ) d θ =

= 1 2 4 θ - cos ⁡ ( 4 θ ) 0 2 π + 1 2 ∫ 0 2 π s e n 2 ( 4 θ ) d θ =

= 4 π + 1 2 ∫ 0 2 π s e n 2 ( 4 θ ) d θ =

Agora precisamos usar essa relação:

sen 2 ⁡ t = 1 - cos ⁡ 2 t 2

Aplicando ao nosso problema, temos:

= 4 π + 1 4 ∫ 0 2 π 1 - cos ⁡ 8 θ d θ =

= 4 π + 1 4 θ - 1 8 sen ⁡ 8 θ 0 2 π =

= 4 π + π 2 = 9 π 2

Resposta

9 π 2

Exercícios de Livros Relacionados

Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.
Encontre a área da região comum aos interiores das cardioides r=1+c o s ⁡ ( θ ) er=1–c o s ⁡ ( θ ) .