Integrais Duplas Impróprias – Intervalos Infinitos
Produzido por Arthur Melo de AlmeidaTeoria
Relembrando o que é integral imprópria
Até agora, você calculou integrais duplas em regiões limitadas (intervalos finitos), certo? A sua região de integração era sempre limitada por um retângulo, arco, parábola, etc , sempre fechada.
Agora, vamos ver como calcular integrais duplas em regiões infinitas.
Lembra quando você viu integrais simples impróprias? Isso aqui:
Lembra disso? A gente tirava o infinito da integral, transformava em um intervalo limitado e resolvia a integral. Depois, era só fazer esse que a gente inventou tender a infinito.
Se o limite existir, essa integral imprópria converge, caso contrário, diverge.
Podia ser isso aqui também:
Nesse caso, a gente fazia tender a .
E, juntando os dois casos:
A gente podia dividir esse intervalo que fosse infinito nas duas direções e, para uma parte, fazíamos o limite ir para e, para outra, .
Beleza, até aí nada novo.
Integrais Duplas em Regiões Infinitas
Vamos, agora, estender esse conceito para duas dimensões. Digamos que você precise calcular essa integral dupla aqui:
A região de integração é uma faixa infinita na direção , percebeu?

Passo 1
Como qualquer ontra integral dupla, vamos começar pela integral de dentro. Vamos separar só para não confundir:
queremos calcular isso aqui:
Isso é uma integral simples qualquer, não é? Vamos usar o que a gente viu lá em cima:
Agora a integral passou a ter intervalo finito e sabemos resolver:
Como , temos que:
Passo 2
Levando isso para nossa integral dupla:
Não mudou muito do que você viu em integrai simples, não é? Você começa pela integral de dentro, fazendo ela ver um intervalo finito. Então, toma o limite desse resultado. O que você encontrar, vai ser seu integrando da segunda integral.
Nesse exemplo, a região era ilimitada apenas na direção , por isso, a segunda integral tinha intervalos finitos. Mas se não tivesse, era sõ você repetir esse passo a passo de novo. Você transformava o intervalo em finito e tomava seu limite.
(Nesse caso do nosso exemplo, se a região fosse infinita nas duas direções, a integral ia divergir.)
Vamos ver uns exercícios agora!
Integrais Duplas em Regiões Infinitas
Exercícios Resolvidos
Exercício Resolvido #1
CEFET - Cálculo 2 - P2 Pericles 2014.2 - 2
Suponha que e sejam variáveis aleatórias com função densidade conjunta e , e nula nos demais casos. Calcule os valores esperados de e .
Passo 1
Bom, antes de tudo, para a gente resolver a questão, precisamos lembrar das seguintes fórmulas da esperança:
Mas, como a nossa questão diz que e , os limites inferiores dessas integrais vão ser zero. Então, precisamos resolver o seguinte:
Passo 2
Vamos começar pela primeira integral, integrando primeiro em relação a :
Agora precisamos relembrar como resolver uma integral imprópria. Usamos o seguinte princípio:
Ou seja, calculamos a integral com intervalo limitado e tomamos o limite do resultado. Beleza? Vamos aplicar isso aqui.
Agora repare que
Então temos:
Agora vamos integrar em relação a usando a mesma ideia:
Vamos fazer integração por partes, fazendo:
Substituindo na nossa expressão, temos:
Agora, como dá uma interterminação , vamos aplicar a Regra de L’Hospital aqui:
Passo 3
Agora vamos resolver a outra integral, usando o mesmo raciocínio.
Então temos:
Agora vamos integrar em relação a usando a mesma ideia:
Vamos fazer integração por partes, como já fizemos, temos:
Resposta
Exercício Resolvido #2
UFRJ – Instituto de matemática, Departamento de Métodos Matemáticos – Exercícios de Integral imprópria (Adaptada)
Encontre o resultado da integral dupla imprópria abaixo:
Onde .
Passo 1
Bem, como em qualquer caso de integral dupla, vamos começar o nosso problema entendendo melhor a região de integração:
- A faixa , significa que a região só pode estar dentro de pedaço
- O problema ainda delimita a faixa pela direita quando ele fala que ...
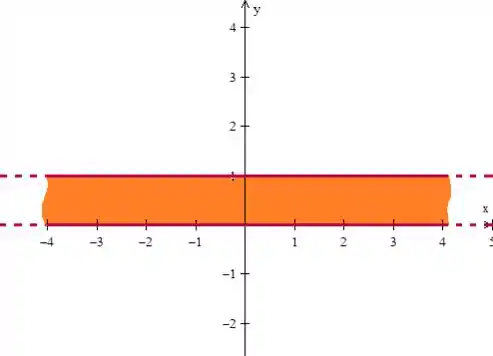
Onde o varia entre e , entende?
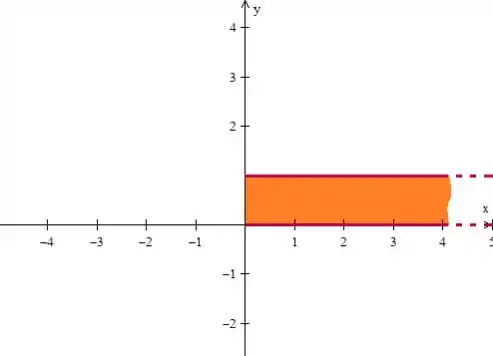
Eis a região 😊!
Passo 2
Você já deve ter notado que a região cresce infinitamente em e esse é o motivo para a integral dupla ser imprópria. Vamos montar aqui essa integral:
Como na região sabemos a variação de e de ...
Basta colocar esses intervalos na integral dupla. MAS ATENÇÃO!!! Na integral mais externa, você deve colocar a variação numérica, que no caso é o intervalo de ...
Veja que como o não tem limite superior, seu limite é o infinito 😉.
Para facilitar os cálculos, tiraremos o infinito da integral e trabalharemos com um limite:
Então agora é só calcularmos a integral dupla mesmo como manda o figurino, ou seja, primeiro a de dentro e depois a de fora. Bora?
Passo 3
Vamos começar com o cálculo da integral de dentro...
Não se assuste com , pois ele é um número qualquer. Pense por exemplo como se ele fosse o número... sei lá, 2. Como a integral é em , é constante...
Para resolvermos essa integral de dentro façamos a mudança de coordenadas...
Derivando em relação a para determinar o ...
Trocando também os limites de integração...
Logo, substituindo tudo na integral...
Substituindo os limites de integração, concluímos que a integral de dentro é...
Passo 4
Pegaremos, em seguida, o resultado anterior e jogar novamente dentro da integral dupla que estamos interessados como faríamos em qualquer integral dupla mesmo...
Como buscamos um limite em (nada a ver com ) podemos tentar tirar o de dentro do limite... Veja bem que...
Então...
Logo, se é constante, o termo pode vazar do limite...
Vamos resolver o limite separado...
Passo 5
Como por propriedade de potência é
Logo...
Passo 6
Por fim, temos que resolver a integral de dentro...
Fazendo uma mudança semelhante a que fizemos anteriormente...
Trocando os limites...
Finalmente, substituindo os limites obtemos...