Integrais Duplas sobre Regiões Gerais
Teoria
Introdução
Para as integrais simples, a região em que integramos é sempre um intervalo, certo? Seja da variável ou . Porém, quando temos duas variáveis, a história já é outra: nosso domínio pode ser diversos tipos de área. Bom você já viu como calcular integrais duplas sobre retângulos, mas e se quisermos integrar em uma região qualquer? Tem um teorema que nos permite fazer isso.
Imagine uma região fechada, representada na figura abaixo em verde. Ela sempre estará contida dentro de um retângulo maior , certo?
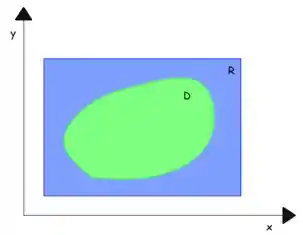
Vamos definir, então, uma função que seja assim:
Sendo assim, podemos dizer que é verdade que:
Pensa bem: nossa função tem valor nulo fora de , portanto, essa região "a mais" não acrescenta nada para a nossa Integral. Não é?
Agora, para calcularmos a integral nessa região, vamos separá-la em integrais simples:
Acontece que, quando nossa região não é um retângulo, não podemos descrevê-la apenas por intervalos de números , , e , pois ela não será limitada por retas, mas sim por funções, curvas como , por exemplo. Ok, e agora? O que fazer?
Sem problemas, digamos que varie entre dois números ( máximo e mínimo) e varie entre as funções e . Quando está fora desse intervalo temos , certo? Enquanto dentro, temos . Assim, podemos escrever a integral em como:
Em resumo, é isso aqui o que você precisa saber! Também podemos escrever como integrais iteradas as integrais duplas em regiões que não são retângulos, a diferença é que teremos funções nos limites de integração para uma das variáveis.
Mas porque apenas para uma das variáveis? Pensa bem, depois que nós resolvermos a integral de dentro, vai sobrar apenas uma integral simples, não é? E os limites de integração de uma integral simples são números! Como você já está cansado de ver. Vamos ver melhor como isso funciona daqui a pouco.
Tipos de regiões
Bom, você acabou de ver que, para integrarmos em regiões gerais, devemos ter uma variável limitada por constantes e a outra, por funções. Agora, é fundamental que você saiba como escrever a região de integração. Para entendermos isso melhor, vamos dividir as regiões em 2 tipos:
Regiões do Tipo I: são as regiões contínuas em , o que significa que precisamos apenas dos valores inicial e final dessa variável ( e ). Neste caso, o intervalo de integração de será dado por duas funções de ( e ). Descrevemos essas regiões assim:
Graficamente, uma região genérica desse tipo é assim:
Você pode pensar dessa forma: em cima e embaixo a região é limitada por funções (as curvas em azul), já na esquerda e na direita, por números (as retas tracejadas). Visualizou?
A integral sobre esse tipo de região é, então, escrita dessa forma (como já vimos):
Exemplo: Calcule , onde é a região entre a parábola e a reta .
Primeiramente, precisamos escrever matematicamente essa região.
Olhando para figura abaixo, vemos que varia entre e (onde a reta e a parábola se encontram), enquanto varia entre as duas funções. Logo, podemos escrever a região como:
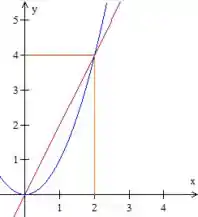
Repara que é maior ou igual à função “de baixo” (em azul) e menor ou igual à “de cima” (em rosa).
Nossa integral passa a ser, então:
Nada demais, né? Beleza, vamos continuar.
Regiões do Tipo II: são o oposto das regiões do tipo I, portanto, contínuas em . Ou seja, em , temos um intervalo definido (números). Já em , a região é limitada por funções. Elas podem ser escritas assim:
O gráfico de uma região genérica desse tipo seria assim:
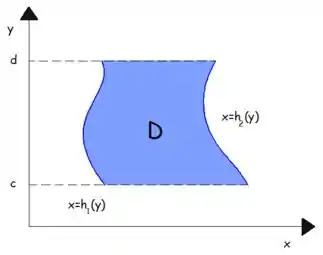
Se você reparar, na esquerda e na direita, a região é limitada por funções (as curvas em azul), já em cima e embaixo, por números (as retas tracejadas).
Com o mesmo raciocínio que usamos nas regiões do tipo I, concluímos que as integrais para as regiões do tipo II podem ser escritas assim:
Exemplo: Calcule , onde é a região entre a parábola e a reta .
Vamos começar tentando esboçar a região . Vamos fazer um esboço para entender melhor a questão. Observando a equação da parábola, vemos que o termo elevado ao quadrado é o , não o , como costumamos ver. Isso quer dizer que essa parábola está “virada de lado”, com eixo de simetria paralelo ao . Como o número que multiplica é positivo, ela está virada para a direita (onde é positivo). Vamos, então, ter algo parecido com isso
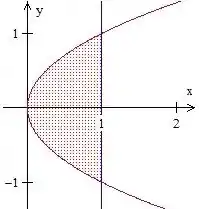
Observe que a interseção entre a reta e a parábola ocorre nos pontos Veja, também, que o é sempre maior ou igual a parábola (a esquerda) e menor ou igual a reta (a direita). Assim, podemos dizer que
OBS: Algumas regiões podem ser escritas tanto como tipo I como tipo II. Nesse caso, você decide a forma que achar mais simples ou melhor para a questão! Em ambos os exemplos podíamos ter optado tanto por tipo I quanto por tipo II.
Cálculo de Áreas
Imagina que queremos calcular a área de uma região . A gente já viu que essa bendita integral dupla representa um volume, certo? Então, mas de um jeito geral os volumes são dados por
Onde é a área da base e é a altura do sólido. Agora, se a nossa altura for 1, ou seja, , vamos ter que o volume coincide com a área da base! Assim, o truque para obter uma área é imaginar um sólido de altura 1 cuja base seja a área que queremos e ai o volume (integral dupla) vai coincidir com a área desejada, ou seja, é só fazer:
Cálculo de Massa
Às vezes a gente quer calcular a massa de uma chapa em forma de parábola, (sim, pessoas estranhas fazem isso). Para fazer isso, vamos precisar da densidade dessa placa que vamos representar por . Só fica atento a uma coisa: normalmente, a gente pensa em densidade como massa sobre o volume. Uma chapa fininha não tem volume, na verdade, essa densidade será massa/área
Onde é a massa da placa e a área da placa. Você já trabalhou muito com densidade em física, mas lá ela era um número constante. Aqui, ela pode variar de ponto a ponto da placa, ou seja, . Então, para calcular a massa de , podemos pensar num elemento bem pequenino (que tal um com área ?) e dizer que sua massa pequenina, , é:
Advinha o que faremos agora? Vamos somar a massa de cada pedacinho para obter a massa da placa toda
A integral acima se resolve da mesma forma que fizemos no exemplo, a diferença é que a função a ser integrada agora é
Beleza? Vamos ver uns exercícios agora!
Tipos de regiões
Cálculo de Áreas
Cálculo de Massa
Exercícios Resolvidos
Exercício Resolvido #1
Lista 21 - UERJ – Cálculo 2 – exercício 3a
Determine o esboço da região do plano sobre a qual a integral é calculada:
Passo 1
Vamos analisar os intervalos de integração que temos para :
No gráfico, é o seguinte:
Passo 2
Agora para :
Isso quer dizer que temos as curvas e limitando nossa região. A primeira, nós sabemos que é uma parábola com concavidade para cima e que passa pela origem, sem grandes novidades:
Agora vamos ver a outra curva, .
Como temos de um lado e do outro, sabemos que também é uma parábola, mas repare no sinal negativo de . Isso significa que a concavidade da parábola está voltada para baixo.
E mais: temos esse termo , que significa que ela está deslocada de alguma forma. Vamos calcular suas raízes para entender melhor:
Ela passa então pelos pontos e . Vamos desenhar isso aqui:
Passo 3
Agora vamos identificar a região:
Beleza? Tranquilo, né?
Resposta
Exercício Resolvido #2
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE Learning, 2010, pp. 920
Calcule
Onde é a região limitada pelas parábolas e .
Passo 1
Primeiramente, vamos fazer um esboço para entender melhor o que está sendo pedido. Como as duas parábolas tem o coeficiente do termo positivos, elas estão viradas para cima. Fazendo , descobriremos suas raízes.
A segunda parábola não possui raízes reais, portanto, não corta o eixo .
Passo 2
Como essa região está limitada em por duas equações (a parábola vermelha e a azul) e em por 2 números, podemos escrevê-la como do tipo I.
Em teremos:
Para descobrir intervalo em , devemos fazer e interseção entre as equações das parábolas e , encontraremos valores.
Assim, descobrimos que varia entre e (onde as curvas se encontram). Podemos, então, escrever a região como:
Passo 3
Vamos, então, substituir em nossa integral os valores que acabamos de encontrar para o domínio.
Cuidado com a ordem de integração!Lembre-se de que as funções ficam na integral de dentro, enquanto os números ficam na de fora.
Passo 4
Agora vamos integrar em relação a (integral de dentro):
Passo 5
Está na hora, então, de integrar em relação a :
Resposta
Exercício Resolvido #3
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 921
Calcule , onde é a região limitada pela reta e pela parábola .
Passo 1
Vamos fazer um esboço para entender melhor a questão.
Observando a equação da parábola, vemos que o termo elevado ao quadrado é o , não o , como costumamos ver. Isso quer dizer que essa parábola está “virada de lado”, com eixo de simetria paralelo ao .
Como o número que multiplica é positivo, ela está virada para a direita (onde é positivo)
Fazendo , vemos que a parábola possui raízes (corta o eixo ):
Agora precisamos analisar a reta. Como o número que multiplica o é positivo, ela está virada para a direita.
O que estamos fazendo é uma análise rápida das equações do domínio, você não deve se preocupar em fazer um gráfico perfeito! Isso é apenas para termos uma noção do formato da área na hora de escrevê-la.
Passo 2
Essa região pode ser escrita tanto como tipo I como II. Porém, no primeiro caso seria preciso dividi-la em duas, pois na esquerda ela está limitada em cima e embaixo pela parábola e na direita, pela parábola e pela reta. Já se escrevermos como tipo II, a questão fica mais simples, pois teremos apenas a parábola na esquerda e a reta na direita.
É importante que você faça essas análises, para evitar contas desnecessárias!
Escrevendo como tipo II, então, precisamos colocar as equações da reta e da parábola em função de , isolando o :
Assim, teremos:
Para encontrar o intervalo de , temos que fazer a interseção entre as duas funções, igualando uma à outra.
Resolvendo
Portanto, temos e nosso domínio será:
Passo 3
Vamos substituir esses valores na integral
Passo 4
Agora vamos integrar em relação a :
Passo 5
Vamos integrar, então, em relação a :
Resposta
Exercício Resolvido #4
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 169
Calcule , onde é o triângulo de vértices (-1,0), (0,1) e (1,0).
Passo 1
Vamos fazer um esboço desse triângulo para visualizar melhor o problema
Passo 2
Devemos, agora, escrever essa região de forma matemática. Perceba varia entre números: e , assim, temos . Já em , essa área é limitada na esquerda pela reta azul e na direita pela vermelha, certo? Assim, podemos escrever essa região como do tipo II, basta encontrar as equações dessas retas.
Para a reta azul
Temos dois pontos que pertencem a essa reta, e , vamos substituí-los na equação geral de uma reta: . Teremos:
Substituindo e , vemos que a reta será escrita como . Porém, como nossa região será escrita como do tipo II, devemos isolar o , ou seja, achar em função de .
Para a reta vermelha
Usando o mesmo raciocínio para descobrir a equação dessa reta, vamos substituir os pontos e na equação geral da reta. Teremos:
Substituindo e , encontramos . Isolando novamente o , teremos:
Assim, o domínio será escrito como:
Passo 3
Agora vamos montar a integral! Basta substituir os intervalos que acabamos de encontrar.
Passo 4
Devemos, então, integrar em relação a :
Passo 5
Vamos integrar, então, em relação a :
Resposta
Exercício Resolvido #5
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009
Suponha que uma lâmina com densidade ocupe a região do plano . Calcule a massa total sabendo que é a região triangular de vértices e a densidade em cada ponto é igual à distância de ao eixo
Passo 1
Sabemos, pela definição de cálculo de massa por integrais duplas, que podemos achar a massa de uma lâmina fazendo a seguinte integral:
Portanto, para resolver esse problema, vamos precisar determinar os limites de integração da nossa região ! Depois é só jogar na integral.
Vamos lá então, o exercício diz que a nossa região é um triângulo com os vértices certo? Mas isso não nos diz muito sobre os limites de integração, vamos ter que achar as retas associadas a esses pontos. No gráfico fica assim:
Perceba também que, quando ele fala que a densidade é igual a distância de cada ponto P ao eixo , o que ele está nos falando é que
Portanto, no final das contas, queremos calcular
Passo 2
Agora que está tudo mais claro, vamos desenvolver o nosso problema. No nosso gráfico temos três retas delimitando a região , duas são mais fáceis de visualizar:
A terceira dá pra descobrir qual é! Sabemos que ela passa pelos pontos e ,né? Então é só usar a equação de qualquer reta:
No ponto (0,0):
No ponto (3,5):
Logo, substituindo e na equação original:
Passo 3
Para o nosso caso em especial não faz tanta diferença determinar os limites de integração como tipo I ou tipo II, vamos fazer aqui então pelo tipo I.
Vendo o gráfico, concluímos que os limites de integração são
Passo 4
Substituindo os valores calculados na integral temos
Passo 5
Resolvendo a integral:
Resposta
Exercício Resolvido #6
PUC-RJ - Cálculo 2 - P1 2015.1 - 1abcd
Seja .
a) Esboce hachurando a região e ao lado a fronteira de .
b) Seja a integral dupla
Escreva na forma iterada, integrando primeiro em relação a e em seguida em relação a .
c) Escreva na forma da soma de duas integrais, integrando primeiro em relação a e depois a .
d) Agora, considere a integral dupla
em que . Calcule pelo método que preferir.
Passo 1
a) Vamos lá, essa é bem direta! Basta pegar as desigualdades que formam e juntá-las!
Olhando pra primeira, temos:
Ela nos diz que, se estamos na curva , que é a parábola que tem a boca apontada para o sentido positivo do eixo e tem extremo na origem, então nossa região se encontra no interior dessa parábola! Andamos para o lado direito pois como é “maior ou igual”, andamos para o sentido do eixo :
Beleza, primeira desigualdade concluída!
Passo 2
Vejamos a segunda:
Ela nos diz que, se temos a reta , então estamos do lado esquerdo da reta (pois, agora, ao contrário da parábola, o é “menor ou igual”!). Colocando essa região no nosso esboço fica:
E, agora que você já está craque nisso, vamos colocar a terceira desigualdade no jogo! Ela é:
Ou seja, se temos a reta , então estamos acima dela, pois é maior ou igual a ela! Juntando no esboço que fizemos até agora, fica:
E, assim, a região é a confluência das três cores:
Aí está o esboço para ! Como pediram também o contorno da região, basta apagar o hachurado de dentro:
Passo 3
b) Agora estão nos pedindo para colocar os limites na integral dupla. Ok, como é pra integrar primeiro em relação a , então deve ser função de e, , por sua vez, deve estar entre duas constantes. Para a parábola, temos . Para a reta, temos . Assim, como está entre a parábola e a reta, vamos ter:
E, para o ? A figura mostrar que ele começa na reta . Para o final, temos que ver qual é o valor no encontro dessas curvas. Para isso, basta fazer:
Resolvendo a equação , temos:
Para o nosso caso, , pois estamos vendo que a coisa toda ocorre sobre o eixo (hehehe), ou seja, . Colocando os limites do , teremos:
E é isso aí :D
Passo 4
c) Bão, agora é fazer exatamente a mesma coisa que o passo anterior, mas estamos com o entre duas constantes e o entre duas funções de .
Neste caso, perceba o seguinte: para estar entre duas funções, precisamos dividir a região entre duas etapas!
Veja, na parte do lado esquerdo, está entre a reta horizontal e a parábola:
E, para essa parábola ser função de , precisamos isolar o :
E, assim, está entre e !
Agora, para a parte da direita, está entre essa reta horizontal e a outra
Transformando a reta vermelha em função de , teremos:
E, assim, está entre e !
Passo 5
Ok, agora que já temos os limites para o , vejamos entre que valores está o !
Olhando a figura como um todo novamente, temos:
E, agora, precisamos descobrir as coordenadas de cada “vértice” de , pois são os pontos onde começam e terminam as duas etapas da divisão que fizemos!
O vértice do lado esquerdo acontece quando a equação da parábola encontra a reta , ou seja:
Pronto! Primeira coordenada de encontrada :D
O vértice de cima acontece quando a parábola encontra a reta vermelha, ou seja, quando , lembra? Colocando em qualquer uma dessas curvas, temos:
E vemos que a coordenada vale para esse encontro!
Finalmente, para o terceiro vértice, teremos o encontro da reta com a reta . Assim, a coordenada é:
Passo 6
Beleza, agora que temos os limites para e , basta montar a integral!
Para a parte da esquerda, está entre e , enquanto está entre e . Assim, nossa integral fica:
E, para a parte da direita, temos entre e , e entre e ! Colocando na integral, teremos:
E para a integral na região toda, temos:
Prontinho, letra detonada!
Passo 7
d) Vamos lá, firmeza que só faltam duas! Vamos tentar resolver aquela primeira que só tinha uma integral? Se ficar difícil tentamos essa soma de integrais que encontramos no passo anterior (mesmo que tenha mais integrais para resolver, pode ser que sejam integrais mais fáceis!).
Colocando a função pedida na integral, teremos:
Integrando em relação a , fica:
Colocando os limites, teremos:
E, agora, podemos dividir essa integral em duas, subtraindo uma da outra:
Passo 8
Vamos lá, para a primeira integral, temos:
Fazendo uma integração por partes,
Resolvendo a integral restante:
E fica:
Fazendo um algebrismo:
Passo 9
Para a segunda integral, teremos apenas que fazer uma substituição simples!
Colocando , teremos e os novos limites de integração serão e :
E fica:
E, juntando esse valor com o da outra integral, teremos:
Resposta
a) Região:
Contorno:
b)
c)
d)