Inversão da Ordem de Integração – Coordenadas Cartesianas
Produzido por Arthur Melo de AlmeidaTeoria
Olá! A inversão de integração é mais um método de resolução de integrais, que podemos aplicar em integrais duplas. Me fala aí, como a gente pode resolver essa integral
Vamos começar pela integral de dentro
Só precisamos integrar em relação a . Mas pera, a função não tem primitiva. Ou seja, é impossível integra-la usando as regrinhas convencionais para integrais simples.
O que faremos? Chorar? Desistir? Não! Lembra que isso é uma integral dupla, por isso, a gente tem mais uma carta na manga: a inversão da ordem de integração!
Mas o que é trocar a ordem de integração? É simplesmente inverter e ? NÃO!! SÓ PODEMOS FAZER ISSO EM REGIÕES RETANGULARES!! Em regiões mais gerais, você tem, também, que reescrever os intervalos de integração. Como assim? Olha só.
Vamos voltar ao exemplo nosso exemplo. Pela montagem da integral, vemos que a região de integração está descrita assim
Essa região está escrita como tipo II ( está entre números e entre funções), inverter sua ordem de integração significa escrevê-la como tipo I. Então precisamos colocar entre funções de , e entre números.
Vamos usar um passo a passo para ver como fica essa inversão? Bora!
Passo a passo
Passo 1: Cara, a primeira coisa é extrair os intervalos de integração da nossa integral. Já fizemos isso
Já vimos que a partir disso, sabemos que queremos agora descrever a nossa região colocando entre números e entre funções.
Passo 2: Aí a gente precisa esboçar essa região que está sendo descrita. Dos intervalos, tiramos essas retas
Nossa região está limitada por todas essas retas ao mesmo tempo. Esboçando
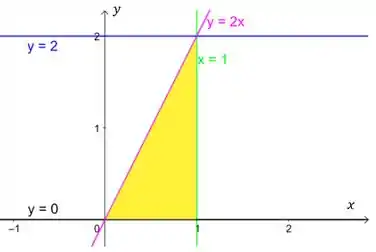
Dica: Como a gente vai limitar entre funções, é sempre bom isolar nessas equações, antes de esboçar. 😉
Passo 3: Olhando para esse esboço, descrevemos nossa região como do tipo I. Vamos colocar entre funções do tipo . Repara que limita nossa região por cima e limita nossa região por baixo, então fazemos
E olhando para o eixo , temos que nossa região está dentro do intervalo
Já que ela começa em , e é limitada pela direita pela reta .
Passo 4: Agora podemos montar a nossa integral com a ordem de integração invertida. Nosso integrando era , ele não muda. Aí a gente integra primeiro em relação a variável que está entre funções, então vamos integrar primeiro em relação a e depois em relação a .
Temos então:
Passo 5: Podemos então calcular essa integral que antes parecia impossível. Não acredita? Vamos fazer a integral de dentro
Como vai ser constante em relação a , podemos tirá-lo da integral. E depois calculando a integral, temos
Fazendo a integral de fora:
Podemos usar a substituição simples , aqui
Viu? Conseguimos calcular!
Na prática
No geral, as questões que envolvem esse método aparecem de duas formas:
(1) O primeiro é esse que vimos. Temos que umas das integrais que forma a integral dupla é impossível de resolver ou muuuuito difícil, aí a gente muda a ordem de integração para ver se cai numa integral dupla mais tranquila de calcular.
(2) O próprio exercício pede para você inverter a ordem de integração. Por exemplo:
Aí o enunciado vai dizer: inverta a ordem de integração dessa integral dupla.
Repara que o domínio de integração não é retangular, ou seja, não temos as duas variáveis da integral entre números. Então, a gente vai precisar usar o nosso passo a passo para entender essa região de integração e fazer a inversão.
Passo 1: Vamos extrair os intervalos de integração da nossa integral.
Percebe que agora quem está entre funções é o , então temos uma região do tipo I. O que a gente vai precisar fazer é descrever nossa região como do tipo II, colocando entre números e entre funções de .
Passo 2: Vamos esboçar essa região que está sendo descrita. Dos intervalos, tiramos
Nossa região está limitada por todas essas retas ao mesmo tempo. Esboçando
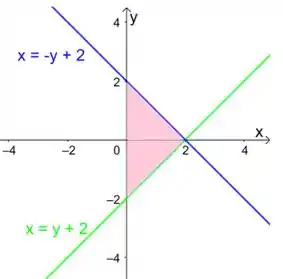
Percebe que como agora a gente vai colocar entre funções de , nós isolamos nas equações que tiramos da integral.
Passo 3: Olhando para esse esboço, descrevemos nossa região como do tipo II. Vamos colocar entre funções do tipo . Mas aqui vai acontecer algo novo, fica atento:
Precisamos limitar nossa região com uma função pela esquerda e com uma função pela direita. Repara que a função que limita nossa região pela esquerda é . Mas agora, olha para a direita, nossa região está limitada por duas retas diferentes, ou seja, por duas funções.
O que fazemos? Cara, vamos ter que dividir nossa região em duas e montar duas integrais, uma para cada função. E na nossa resposta essas integrais aparecem somadas. A gente vai dividir a região original em , que é onde temos a interseção dessas duas funções.
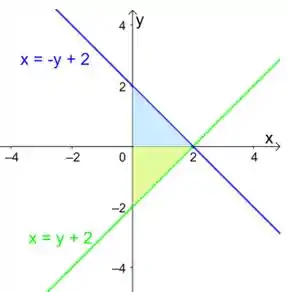
Agora sim, cada região está limitada pela direita por só uma função. Temos que para a região em azul
Nossa região está limitada pela direita pela função e pela esquerda por :
Já para a região verde, temos que , a limita pela esquerda e a limita pela direita:
Passo 4: Agora podemos montar a nossas integrais. Mantemos o nosso integrando. Aí a gente integra primeiro em relação a variável que está entre funções, então vamos integrar primeiro em relação a e depois em relação a .
A integral para a região verde é
E para a azul:
Então é a reposta final é
Prontinho! Agora partiu exercitar! 😊
Passo a passo
Na prática
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria.
Troque a ordem de integração para calcular
Passo 1
A região está escrita como tipo II, temos e . Antes de trocar essa ordem de integração, vamos fazer um esboço desse domínio.
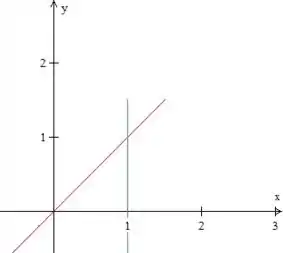
Passo 2
Para escrever a região como tipo I, teremos variando entre números. Pelo próprio gráfico, vemos que:
Pela figura, vemos também, que o limite inferior de é (o eixo ), falta então, descobrir o superior. Para isso, basta escrever a equação da reta vermelha em função de , o que é bem simples. Em vez de termos , teremos .
Então, o domínio passa a ser
Passo 3
Vamos, agora, levar esses valores para a integral, invertendo a ordem .
Passo 4
Começaremos integrando em relação a :
Passo 5
Agora vamos integrar em relação a , fazendo a substituição .
Resposta
Exercício Resolvido #2
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 922
Calcule a integral iterada
Passo 1
Vamos esboçar essa região de integração, que é bem simples. Repara que temos como limites de a curva e a curva , enquanto varia de a
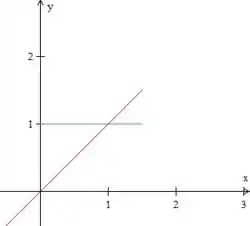
Passo 2
Analisando a questão, percebemos que temos um problema: . Não sabemos calcular essa integral, por isso, usaremos um artifício para fugir dela, inverter a ordem de integração. Precisamos, então, reescrever a região acima como tipo II.
Pelo gráfico, vemos que varia entre e e que varia entre e a reta vermelha (). Pronto, basta levar esses valores para a integral de forma invertida, teremos:
Você verá que essa troca facilitará muito nossa vida!
Passo 3
Vamos integrar, então, em relação a :
Passo 4
Agora, vamos integrar em relação a , fazendo a substituição . Temos .
Resposta
Exercício Resolvido #3
USP - Cálculo 3 - P1 - 2013 – 1a
Calcule a seguinte integral:
Passo 1
Vamos esboçar essa região de integração. Temos variando de até e desde até :
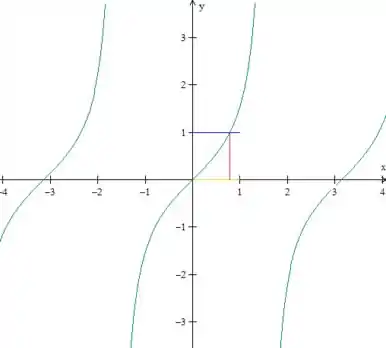
Nossa região de integração é, portanto:
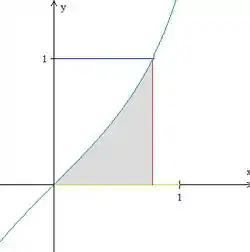
Passo 2
Analisando a questão, percebemos que temos um problema: . Não sabemos calcular essa integral. Por isso, usaremos um artifício para fugir dela, inverter a ordem de integração. Precisamos, então, reescrever a região acima como tipo I.
Pelo gráfico, vemos que varia entre e o e que varia entre e a curva verde (). Pronto, basta levar esses valores para a integral de forma invertida, teremos:
Você verá que essa troca facilitará muito nossa vida!
Passo 3
Vamos integrar, então, em relação a :
Passo 4
Agora, vamos integrar em relação a . Primeiro vamos abrir essas funções trigonométricas
Sabemos que
Logo,
Fazendo , vamos obter
Aplicando os limites temos:
Resposta
Exercício Resolvido #4
UFRJ - Cálculo 3 - P1 2011.1 – 1a
Considere a seguinte integral dupla
- Reescreva a integral com a ordem de integração invertida, sendo .
Passo 1
É muito importante esboçar essa região, para podermos visualizar melhor o problema. Vamos começar analisando o intervalo de , repare que o limite superior é . Se elevarmos os dois lados ao quadrado, passamos a ter:
Essa é a equação de uma circunferência de raio . Como a raiz tem que ser positiva, vamos desenhar apenas a parte com .
A outra equação que limita é (ou ), que nada mais é do que uma reta de coeficiente angular igual a – ou seja uma reta com ângulo de inclinação igual a – que desenhamos abaixo em azul.
Agora vamos analisar os limites de : temos e , ou seja, dois números. Mas não é um valor qualquer de , é exatamente o ponto em que a reta corta a circunferência, pois:
Assim, o ponto satisfaz as duas equações.
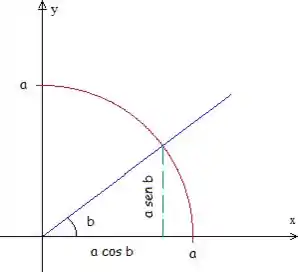
A região de integração é limitada pela reta na esquerda e pela circunferência na direita.
Passo 2
Para reescrever a região acima como tipo I, precisaremos dividi-la em duas, pois a região à esquerda de , é limitada superiormente pela reta azul, mas a direita é limitada pela curva em vermelho. Como não temos uma continuidade, vamos chamar a parte da esquerda de e a da direita de .
Para
O intervalo em dessa região vai de até , onde , portanto, temos . Em , temos embaixo e a reta azul em cima. Assim, esse domínio será da seguinte forma:
Perceba que escrevemos a equação da reta em função de .
Para
Os limites de dessa região são e , o que significa: . Em , temos novamente embaixo, mas agora, a parte de cima é limitada pela circunferência, então vamos escrever sua equação em função de .
(Apenas a parte com nos interessa)
Podemos, então, escrever esse domínio como:
Passo 3
Finalmente, podemos reescrever a nossa integral: