Valores Médios em Regiões Planas
Produzido por Arthur Melo de AlmeidaTeoria
Introdução
Quando pensamos em médias, pensamos logo naquela média clássica em que somamos os valores e depois dividimos pelo números de termos, né?
O que vamos fazer aqui não é tão diferente disso, mas como estamos estudando integrais duplas, temos que extender um pouco nosso conceito, vamos ver!
Imagina um caso assim:

Bem, essa aqui todo mundo sabe, é só fazer , que dá , e dividir pelo total de termos, nesse caso 4, que temos a média dessa região aí: .
Calma, eu sei que esse é muito fácil... Mas acho que com esse exemplo bobo já dá pra ver alguns conceitos importantes:
1º: Temos a soma de todos os valores. Para uma função, “somar todos os valores” nada mais é do que integrar. Nesse caso, a integral dupla de sobre a uma região qualquer:
2º: Depois, temos o números de termos. Isso é um pouco mais estranho, mas eu gostaria que você reparasse que, naquele exemplo que temos ali em cima, o número total de termos é exatamente igual a área do nosso quadrado . E é basicamente isso que vamos usar no denominador, a área da região.
Para regiões tranquilas, tipo quadrados, triângulos e círculos, podemos usar as fórmulas matématicas que vimos lá no ensino fundamental... haha. Mas, para regiões estranhas e totalmente gerais, podemos usar a integral dupla. Lembrando:
Por fim, chegamos na nossa fórmula bonitinha:
Sem mistério! Vamos só ver um exemplo pra deixar tudo bem claro!
Exemplo
Encontre o valor médio da função , sobre a região limitada pelas retas , e .
Passo 1: Montar o problema
O problema é bem claro sobre o que ele quer, então sabemos que temos que usar nossa fórmula:
Então é só calcular cada um desses termos aí. Mas antes, vamos entender nossa região aqui.
Passo 2: Descrever a região
A nossa região é basicamente:
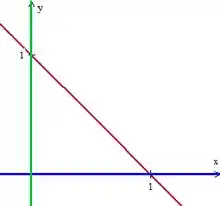
Que pode ser descrita como Tipo assim:
Então já podemos fazer a integral aqui!
Passo 3: Calcular a integral dupla do numerador
Vamos ter:
E agora só falta a área.
Passo 4: Calcular a área da região
Por sorte, a região é bem fácil de acharmos a área, pois temos um triângulo. Então não vamos ter que integrar nem nada, vamos ter simplesmente:
Só vamos dividir agora.
Passo 5: Dividir os dois termos
Finalmente, vamos ter:
Pronto, nada bizarro, né?
Essas questões tem um passo a passo muito bem defindo:
Passo 1: Montar o problema, colocando a nossa fórmula do valor médio;
Passo 2: Descrever a região, determinando os limites de integração;
Passo 3: Calcular a integral dupla da função ;
Passo 4: Calcular a área da região;
Passo 5: Dividir os termos calculados no passo 3 e 4, de acordo com a fórmula do valor médio.
Agora vamos ver os exercícios pra fixarmos bem essa ideia!
Exemplo
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009
Encontre o valor médio de sobre o retângulo ,
Passo 1
Acabamos de aprender esse tipo de questão, né? Você vai perceber que é um método de resolução bem pratico, é só seguir o passo a passo do final da teoria!
O passo 1 nos diz para montarmos o problema né? Vamos colocar a fórmula do valor médio aqui e pensar no que precisamos calcular de forma organizada.
Portanto precisamos definir a nossa região , que nesse caso é um retângulo. Em seguida calcular a integral dupla de e, por fim, calcular a área dessa região! Depois é só voltar pra fórmula e substituir os valores, vamos lá?
Passo 2
Nossa região é bem simples de se definir, vai ser um retângulo cujos limites já estão explícitos no enunciado, então esse passo vai ser só pra gente deixar indicado mesmo quais são nossos limites de integração:
Passo 3
Definida a nossa região, podemos agora fazer a nossa integral para a função
A ordem de integração aqui não influencia muito nas contas nenhuma, vamos fazer aqui o tipo , mas sinta-se a vontade se preferir o outro tipo!
Integrando em :
Integrando em :
Passo 4
Vamos agora calcular o outro termo da fórmula do valor médio: a área da região . Perceba que aqui, caso tivéssemos alguma região muito complicada teríamos que fazer outra integral dupla, certo? Só que, nesse exercício, a região é um retângulo, que tem área definida como base vezes altura!
Qual vai ser nossa base e nossa altura então? São os limites de e ! Não precisa nem esboçar, mas se você quisesse ver, nossa região é isso aqui:
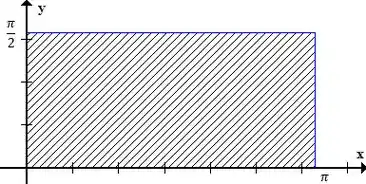
Passo 5
Portanto, juntando os valores que calculamos nos passos 3 e 4 e, voltando para aquela fórmula lá do começo, vemos que:
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009
Encontre a altura média do paraboloide sobre o quadrado ,
Passo 1
Essa questão é um pouco diferente, né? Não vimos em nenhum exemplo anterior como calcular uma altura média. Vamos tentar entender melhor o que o enunciado está pedindo.
A partir do momento que ele fala da média de uma função contínua, nos faz imaginar que vamos precisar usar a fórmula do valor médio
Beleza, só precisamos então escrever a altura do paraboloide como uma função de e ! E como faremos isso?
De certa forma, a gente já se acostuma a ver o eixo como a altura de alguns objetos, isso porque ele está “meio que” pra cima em todas as questão, com isso, não é muito difícil imaginar a altura como a própria equação do paraboloide!
Agora ficou mais simples, certo? Temos a nossa função e o nosso domínio definido pelo enunciado, é só calcular a integral dupla e a área pra chegarmos na resposta! Vamos lá?
Passo 2
Como nosso domínio já está definido no enunciado, podemos ir direto para o cálculo da integral dupla. Nesse caso, tanto faz a ordem de integração que escolhermos, fazendo pelo tipo então:
Integrando-se em :
Integrando-se em :
Passo 3
Vamos agora analisar a área da nossa região . Note que o enunciado mesmo já nos diz que é um quadrado! Bem tranquilo, né? Nesse caso o nosso quadrado tem lado igual a , portanto:
Passo 4
Pronto, calculada a integral dupla e a área de , é só juntar tudo na fórmula do valor médio.
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule a temperatura média de uma placa limitada pelos eixos cartesianos e pelas retas , sabendo que a temperatura em cada ponto obedece a função
Passo 1
Vamos organizar as informações que o problema deu pra gente e entender o que precisamos fazer. O enunciado pediu pra calcular uma temperatura média, certo? Então já imaginamos que vamos ter que usar a fórmula do valor médio:
No caso a nossa função vai ser a da temperatura dada:
Precisamos então determinar os limites da nossa região para poder calcular a integral dupla de e, por fim, calcular a área de , vamos lá?
Passo 2
Vamos descrever a nossa região , graficamente ela é assim:
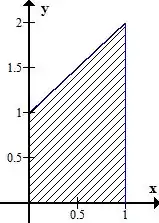
A maneira mais fácil de escolher os limites de integração vai ser pelo tipo , nesse caso, definimos como o intervalo entre zero e a função
Passo 3
Beleza, definidos os limites, podemos pensar na nossa integral dupla, lembrando que a função que o enunciado deu foi
Integrando em , vamos considerar como constante, com isso:
Para fazer essa integral aí, vamos ter que aplicar uma mudança de variável, fica assim:
Substituindo tudo isso, temos que:
Passo 4
Calculada a nossa integral dupla, vamos continuar o passo a passo calculando a área da região . Nessa questão aqui tem dois jeitos de fazer, vou mostrar os dois e você escolhe qual achou mais simples, beleza?
O primeiro é o que vai dar certo sempre! Aquele que, mesmo que o enunciado te dê a região mais bizarra do mundo a gente consegue calcular a área: pela integral dupla!
O segundo jeito é mais visual, percebe que a nossa região pode ser dividida em um quadrado e um triângulo assim:
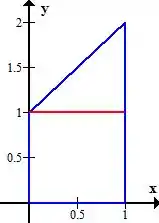
O quadrado tem lado igual a , portanto sua área é simples de calcular.
O triângulo tem base e altura iguais a também, portanto, podemos calcular a área da região como a soma das duas áreas!
Passo 5
Temos então o valor da integral e da área da região, agora é só jogar esses valores na fórmula do valor médio!