Centro de Massa e Centroide de Sólidos
Produzido por Arthur Melo de AlmeidaTeoria
Centro de Massa
Como já vimos para as regiões planas, podemos entender o centro de massa de um corpo como o ponto em que podemos considerar que toda a sua massa se concentra.
Como assim? Se nós temos um corpo de três dimensões (um cubo, por exemplo) e queremos tratá-lo em um problema como uma massa pontual, esse ponto deve ser o centro de massa.
Beleza, agora vamos escrever isso matematicamente. Sendo a densidade de massa desse volume, nós sabemos que sua massa é dada pela integração dessa função na região volumétrica ocupada por esse corpo:
O primeiro momento em relação ao plano é dado pela integração dessa densidade multiplicada pela distância de cada ponto da placa ao plano (repare que essa distância é exatamente igual a ). Portanto:
Você pode interpretar essa expressão como , ou seja, a soma de cada diferencial de massa da placa multiplicado pelo seu braço de alavanca .
O momento em relação ao plano segue o mesmo raciocínio, a distância de cada ponto da placa a esse eixo será dada por :
Para o plano , a distância é :
Então, nós temos que as coordenadas do centro de massa são dadas por:
Você pode pensar nessas expressões como médias ponderadas, onde o peso é a massa da placa. Como assim?
não é dado pela multiplicação, em cada ponto do sólido, entre a massa do ponto e a coordenada ? Se nós somamos para cada ponto do sólido e dividimos pela massa total do mesmo, nós temos uma “coordenada média”, certo? Esse é o conceito de centro de massa.
Para ficar mais fácil de memorizar aquelas expressões pense no seguinte: o denominador é sempre a integral da densidade no volume (o que nos dá a massa), enquanto o numerador é a integral dessa densidade multiplicada pela coordenada do centroide que queremos.
Bom, nesse tipo de questão, então você precisa basicamente encontrar a massa da região e o momentos momentos e e, em seguida, fazer a relação entre esses valores.
Para cara uma dessas grandezas você terá que montar e resolver uma integral tripla, usando os mesmos conceitos que você já conhece.
Centroide
Definimos o centroide como o centro geométrico de uma região. Como assim?! Calma, da mesma forma que o centro de massa pode ser interpretado como uma média ponderada onde o peso é a massa da região, podemos ver o centroide como uma média onde o peso é o volume.
Seguindo esse mesmo raciocínio, nós temos o volume de uma região :
Então, as coordenadas do centroide de uma região plana são dadas por:
Viu que é muito parecido com o centro de massa, não é? Repare que quando , as expressões são exatamente iguais. Isso quer dizer que, em regiões com densidade constante, homogênea, o centro de massa e o centroide (centro geométrico) coincidem.
Esses dois tipos de questão são extremamente parecidos. O passo a passo é o mesmo, a diferença será se a densidade aparecerá ou não nas expressões.
Você vai montar essas quatro integrais (pense nas médias ponderadas para se lembrar das fórmulas) e resolvê-las como qualquer outra integral tripla que você já fez: usando mudança esférica, cilíndríca, etc quando necessário. Vamos ver um exemplo
Exemplo: Determine o centro de massa do cubo , , , cuja densidade no ponto é .
Passo 1: Como nós sabemos, as coordenadas do centro de massa de um sólido são dadas por:
Onde são momentos e é a massa total do sólido. Então, vamos calcular cada um desses termos separadamente.
Passo 2: Primeiro, vamos calcular a massa . Se a função densidade é , então
Como é um cubo, podemos escrever direto , e na integral:
Resolvendo isso aí, temos
Passo 3: Agora vamos calcular os momentos.
Substituindo os intervalos:
Passo 4: Agora o
Substituindo os intervalos:
Passo 5: Por último o
Substituindo os intervalos:
Passo 6: Show, agora vamos juntar isso tudo para encontrar o centro de massa:
O conceito novo desse capítulo basicamente são essas fórmulas! O resto você já conhece. Vamos treinar um pouco agora!
Centroide
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP - Cálculo 2 - P2 2014 Noite – 4
Determine o centro de massa do cubo , , , cuja densidade no ponto é .
Passo 1
Como nós sabemos, as coordenadas do centro de massa de um sólido são dadas por:
Onde são momentos e é a massa total do sólido. Então vamos calcular cada um desses termos separadamente.
Passo 2
Primeiro, vamos calcular a massa . Se a função densidade é , então
Como é um cubo, podemos escrever direto , e na integral:
Resolvendo isso aí, temos
Passo 3
Agora vamos calcular os momentos.
Substituindo os intervalos:
Passo 4
Por último
Substituindo os intervalos:
Passo 5
Temos:
Substituindo os intervalos:
Passo 6
Show, agora vamos juntar isso tudo para encontrar o centro de massa:
Resposta
Exercício Resolvido #2
George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil ltda., 2009, pp. 436-13.
Seja uma região sólida no primeiro octante é limitada pelos planos coordenados e pelo plano . A densidade do sólido é . Encontre a massa do sólido e o centro de massa.
Passo 1
Primeiro vamos determinar os limites das variáveis, o solido é
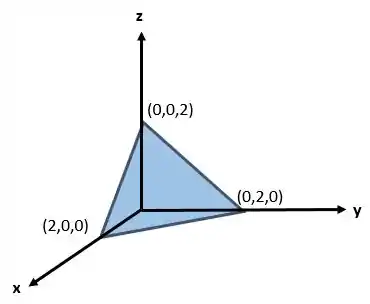
Então vamos começar fazendo,
Ao fixar um valor de , temos que vai variar da seguinte forma
Para entender isso, vamos olhar o plano , ele é limitado pelos eixos coordenados e pela reta Agora para um ponto determinado, a varável vai variar da seguinte forma
Agora que já temos os limites das variáveis no sólido, vamos ir para as integrais que usamos para calcular a massa e o centro de massa!
Passo 2
A massa do sólido é dada por,
Passo 3
Agora vamos calcular os momentos,
Como a equação é simétrica em e , ou seja, se trocarmos por e vice versa as equações não se alteram, temos que
Agora, por último temos
Passo 4
Já temos os momentos, agora vamos encontraro centro de massa:
Assim,
Resposta
Exercício Resolvido #3
George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education do Brasil ltda., 2009, pp. 451-67.
Um sólido de densidade constante é limitado abaixo pelo plano , acima pelo cone , e dos lados pelo cilindro . Encontre o centro de massa.
Passo 1
Como temos um sólido limitado por um cilindro, vamos usar as coordenadas cilíndricas para resolver nosso problema! As coordenadas cilíndricas são e .
Pelos limites do sólido temos que
Pelos lados dentro do cilindro ,
Agora falta a variável ,
Pronto, agora vamos calcular a integral que no da a massa e o centro de massa!
Passo 2
Para calcular o centro de massa precisamos encontrar a massa do sólido e os momentos! Como a densidade é constante e não sabemos seu valor, vamos chamas ela de . Em coordenadas cilíndricas a massa é dada por,
Passo 3
Agora o calculo dos momentos,
Como o sólido é simétrico em relação ao eixo , temos que
Para determinar o centro de massa falta a coordenada :
Assim,
Resposta
Exercício Resolvido #4
Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1085 – 29
Use coordenadas cilíndricas para encontrar o centroide do sólido limitado acima pela esfera
E abaixo pelo paraboloide
Passo 1
Como vamos usar as coordenadas cilíndricas para resolver nosso problema! As coordenadas cilíndricas são e .
Se quiser visualizar melhor o problema, o esboço é esse aqui
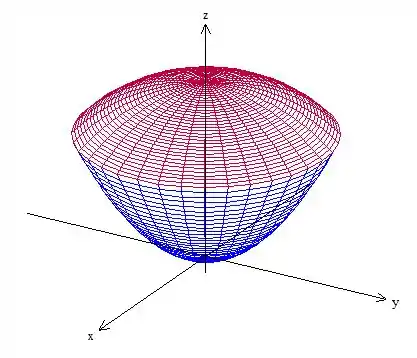
Passo 2
Agora devemos encontrar os limites das variáveis, para isso vamos determinar os limites das variáveis e para isso precisamos da intercessão entre a esfera e o paraboloide:
Substituindo a equação do paraboloide na equação da esfera temos,
Esta equação tem raízes e
Como , ou seja, a soma de dois quadrados, tem que ser positivo pois estamos trabalhando com números reais. Logo,
Passo 3
Assim, temos que, ao usar as coordenadas cilíndricas:
Para a variável , seus limite superior é a esfera, logo
Seu limite inferior é dado pelo paraboloide, logo
Assim,
Para a variável ela vai variar ate no máximo o valor da intercessão entre a esfera e o paraboloide, lembra que encontramos esse valor lá em cima? A interseção das superfícies é dada em
Com isso,
Por último,
Passo 4
Vamos calcular o centróide agora!! Como o sólido é simétrico em relação ao eixo , temos que
Para calcular vamos usar a fórmula:
Calculando o volume,
Vamos calcular a integral
Assim,
O centóide será,
Resposta
O centroide será