Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 25

Utilize coordenadas esféricas.

Determine o centroide do sólido do exercício 25.

Passo 1

Oi, galera! Tudo bom?

Nossa questão pede para acharmos o centroide do sólido do exercício 25;

O sólido do exercício 25 é limitado pelo plano x z e pelos hemisférios

y = 9 - x 2 - z 2

e

y = 16 - x 2 - y 2

Só lembrando que o centroide é o ponto de centro de massa de um sólido.

Como o centroide é um ponto, ele vai ter coordenadas ( x - , y - , z - ) . O cálculo do centroide é dado pelas seguintes integrais:

x - = 1 V ∭ D x   d V

y - = 1 V ∭ D y   d V

z - = 1 V ∭ D z   d V

Onde V é o volume do sólido.

Então, o que precisamos fazer aqui para resolvermos essa questão é calcular cada uma dessas integrais usando coordenadas esféricas. Lembra que estamos usando o exercício 25 que já temos a resolução, então vamos aplicar diretamente os limites de integração que já achamos lá (dá uma olhadinha nele caso precise).

Também vamos precisar calcular nosso volume V do sólido e podemos achar nosso centroide. Lembrando que o volume de hemisfério (metade de uma esfera) é:

V = 1 2 4 3 π r 3

Bora lá!

Passo 2

Um breve resumo dos limites que detalhamos no exercício 25: Note que podemos descrever a região entre esses hemisférios fazendo

3 ≤ ρ ≤ 4

Como o sólido é limitado pelo plano x z , devemos ter que o ângulo polar só varre os dois primeiros quadrantes:

0 ≤ θ ≤ π

Como z pode ser negativo, o ângulo azimutal varia livremente:

0 ≤ ϕ ≤ π

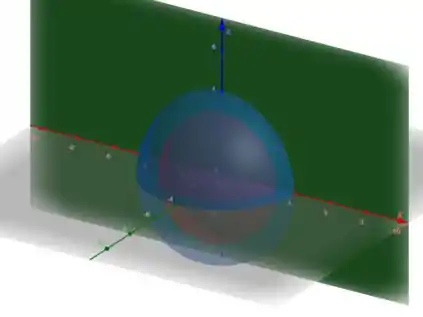
Passo 3

Agora, vamos pensar nas nossas integrais da coordenada do centroide.

Devido a simetria com relação ao plano x z , as componentes x e z do centroide serão nulas:

x - = z - = 0

Supondo que a distribuição de massa do sólido é uniforme (sólido homogêneo), a integral que vamos precisar calcular é:

y - = 1 V ∭ D y   d V

Usando que

y = ρ   s e n   ϕ   s e n   θ

temos que

y - = 1 V ∫ 2 3 d ρ ∫ 0 π d θ ∫ 0 π ρ 3   s e n 2 ϕ   s e n   θ   d ϕ

Portanto

y - = 1 V ∫ 3 4 ρ 3   d ρ ∫ 0 π s e n   θ   d θ ∫ 0 π s e n 2 ϕ   d ϕ

Calculando cada integral:

∫ 0 π s e n   θ   d θ = - cos ⁡ θ 0 π

Aplicando os limites de integração:

- cos ⁡ θ 0 π = 2

Integral de ϕ :

∫ 0 π s e n 2 ϕ   d ϕ

Usando a identidade:

s e n 2 ϕ = 1 - cos ⁡ 2 ϕ 2

Substituindo, integrando e aplicando os limites de integração:

= ∫ 0 π 1 - cos ⁡ 2 ϕ 2   d ϕ = π 2

Por último, integramos em ρ e aplicamos os limites:

∫ 3 4 ρ 3   d ρ = 1 4 3 4 - 2 4

Calculando nosso valor:

= 1 4 256 - 81 = 175 4

Assim, podemos substituir na integral:

y - = 1 V ⋅ 227 4 ⋅ 2 ⋅ π 2

Simplificando:

y - = 1 V ⋅ 175 π 4

Passo 4

Agora é só calcularmos o valor de V . O volume será a metade da região entre as esferas, como a gente esquematizou na imagem do passo 2:

V s ó l i d o = V h e m i s f é r i o   m a i o r - V h e m i s f é r i o   m e n o r

Como o volume de uma meia esfera é dado por:

V = 1 2 4 3 π r 3

Teremos:

V s ó l i d o = 1 2 4 π 3 ⋅ 4 3 - 4 π 3 ⋅ 3 3

Calculando:

= 2 π 3 64 - 27 = 74 π 3

Portanto, nossa coordenada será:

y - = 3 74 π ⋅ 175 π 4 = 525 296

Como já vimos, as demais coordenadas são nulas, então:

x - , y - , z - = 0 , 525 296 ,   0

Resposta

x - , y - , z - = 0 , 525 296 ,   0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Centro de massa, momento de inercia: encontre o centro de massa e o momento de inercia em relação ao eixo x de uma placa retangular fina delimitada pelas retas x = 0 , x = 20, y = - 1 e y = 1 se δ x ,
Encontrando um centroide: encontre um centroide da região do primeiro quadrante delimitado pelo eixo x, a parábola y 2 = 2 x e a reta x + y = 4 .
Centro de massa, momento de inércia: encontre o centro de massa e o momento de inercia em relação aos eixos coordenados e o momento de inercia polar de uma placa triangular fina delimitada pelas retas
Centroide de uma região infinita: encontre o centroide de uma região infinita no primeiro quadrante delimitada pelos eixos e pela curva y = e x . (Utilize integrais improprias nas formula de massa)
Encontre o centro de massa e o momento de inercia em relação ao eixo y de uma placa fina delimitada pela reta y = 1 e a parábola y = x 2 se a densidade for δ x , y = y + 1 .