Mudança da Ordem de Integração em Integrais Triplas
Produzido por Arthur Melo de AlmeidaTeoria
Esboço de sólidos
Cara aqui vamos ter que desenhar certas figurinhas!
Relaxa que ninguém precisa ser um artista para fazer um bom esboço! A questão chave entre um bom desenho e um que a gente não entende muito bem é saber escolher as projeções convenientes! Não adianta a gente desenhar todas as curvas se, no final, não conseguimos entender o nosso sólido, né?
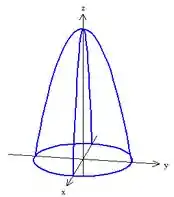
Esse aqui é um exemplo de um bom esboço com poucos traços, na prova você não perde mais do que 5 minutos para fazê-lo e dá pra visualizar perfeitamente de qual sólido estamos falando, certo? Nesse caso um paraboloide
Escolha das projeções convenientes
Vamos tentar entender, então, como escolher as melhores projeções para fazer um bom esboço! De forma bem prática, 99% das vezes as melhores curvas vão ser quando projetarmos o sólido nos planos , ou , ou seja, quando fazemos , e , respectivamente. Aquele 1% que não for exatamente esses planos ainda vai ser bem parecido, relaxa.
Quando projetamos o sólido nesses planos, ficamos sempre com curvas bem definidas de duas variáveis, você lembra das equações das principais curvas? (Reta, parábola, circunferência, hipérbole). Se não lembrar tudo bem, vamos fazer uma revisão disso aqui bem rápida!
Reta: Na equação da reta, você vai encontrar os seus dois termos sem nenhum expoente (vamos escrever como e mas também pode ser e , ou e ). Sendo que ela pode estar na forma explícita:
Ou na forma implícita:
Parábola: Aqui vamos ter uma equação de segundo grau comum, geralmente ela é encontrada assim:
Circunferência/Elipse: Aqui vamos ter os dois termos elevados ao quadrado, se somando e divididos por duas constantes:
Obs: Quando temos uma circunferência de raio . Se , temos uma elipse
Hipérbole: Aqui vamos ter os dois termos ao quadrado também, só que dessa vez eles vão estar se subtraindo! De forma geral:
Exemplos
No exemplo lá do começo do capítulo, percebe que só existem três curvas compondo o esboço do sólido!
Na primeira temos :
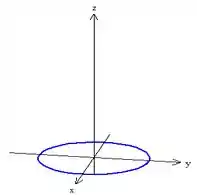
Na segunda temos
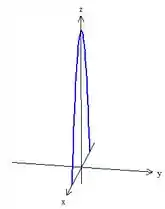
Por fim, na terceira curva temos
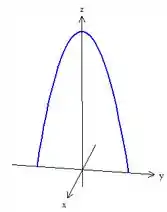
Simplesmente desenhando as três curvas juntas, obtemos o sólido lá de cima:
Pronto, bem simples né? Resumindo, para fazer um bom esm boço de sólido, precisamos escolher as curvas certas! Geralmente vão ser as projeções sobre os planos cartesianos!
Mudança da Ordem de Integração
Até agora em integrais triplas, vimos como calcular várias integrais triplas em regiões cúbicas, em regiões gerais e como esboçar sólidos. Vamos aprender agora uma nova técnica: a mudança da ordem de integração.
Vem comigo nesse exemplo aqui
Passo 1: Perceba que, na ordem que o exercício propõe, não conseguimos calcular a integral de , vamos então inverter essa ordem pra ver como fica.
Eu posso só ir invertendo as integrais lá em cima? NÃÃÃO!!! Vou te ensinar como faz
Primeiro, vamos precisar de um esboço do nosso sólido, beleza?
Pelos limites das integrais sabemos que:
Então o sólido fica assim:
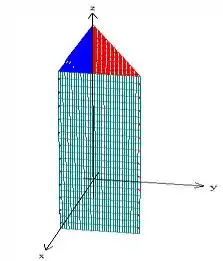
Passo 2: Se a dificuldade é integrar , vamos tentar integrar alguma outra variável antes para ver se fica mais fácil. Vamos inverter então a ordem para , dessa forma vamos integrar antes de .
Para fazer isso vamos ter que redefinir os intervalos de integração! Perceba que temos um plano , podemos escrevê-lo novamente como:
Graficamente nosso intervalo no plano é:
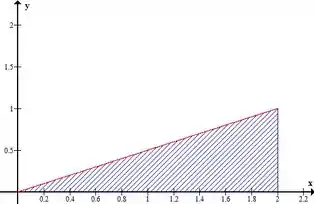
Dessa forma, temos que
Nesse caso não precisamos mudar nada no , então seu intervalo continua
Passo 3: Reescrevendo nossa integral:
Passo 4: Integrando em
Passo 5: Agora vamos conseguir integrar em ! Fazendo a substituição de
Passo 6: Integrando em z
Ficou até bem simples, né? Alguns exercícios vão te pedir diretamente algo do tipo “Inverta a ordem de integração de para ”, então já sabe, para fazer isso precisamos:
Passo 1: Reconhecer os limites do sólido dado e esboçar o gráfico
Passo 2: Perceber o melhor tipo de integração (I, II ou III), ou o tipo que a questão pedir, e determinar os novos limites
Passo 3: Reescrever e calcular a integral
Vamos dar uma praticada nisso? Parte pros exercícios resolvidos aí!
Exemplos
Mudança da Ordem de Integração
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009 - Modificado
Esboce o gráfico associado à seguinte integral:
Passo 1
Vamos especificar primeiro os limites que podemos tirar a partir das integrais. Pela integral de fora:
Pela integral do meio:
Pela integral de dentro:
Passo 2
Vamos analisar os nossos dois primeiros limites. Perceba que eles estão no plano sendo que, em , vamos ter essas duas curvas:
Graficamente isso fica assim:
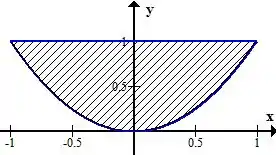
Passo 3
Tendo determinado a região em duas dimensões, vamos expandi-la para a terceira, no nosso caso, o eixo .
Pelo passo 1, vemos que está limitado pelos planos e . Em três dimensões e limitados pela região encontrada no temos o seguinte:
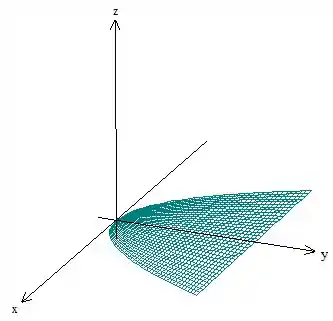
Agora para o plano também limitado por aquela região em :
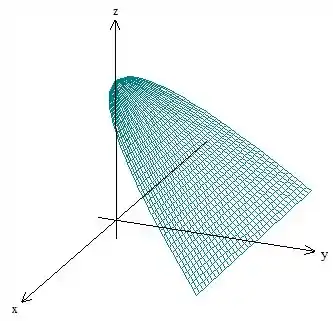
Perceba que ambos os planos existem em outros pontos, só que só queremos a região expandida em relação àquela encontrada no !
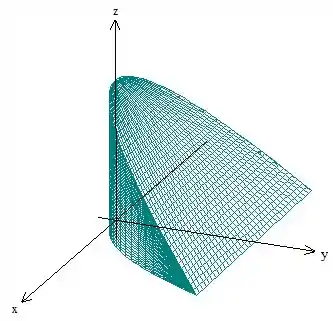
Pronto, agora é só ver qual o sólido que está entre essas regiões. Fica assim:
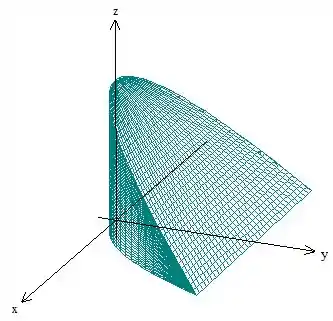
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009
Calcule a integral, mudando a ordem de integração de forma apropriada
Passo 1
Assim como aconteceu no exemplo da teoria, vemos que não conseguiríamos integrar direto em função de . Portanto, vamos ter que integrar alguma outra variável antes, certo?
Vamos antes entender o nosso sólido:
Esboçando esses limites temos:
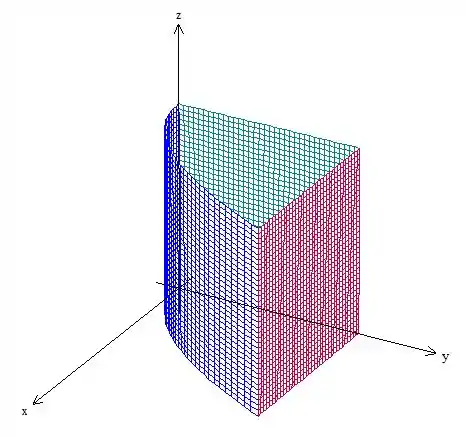
Passo 2
Como não queremos integrar em , vamos mudar a ordem de integração para
No plano , tínhamos limitado por
E limitado por
No plano :
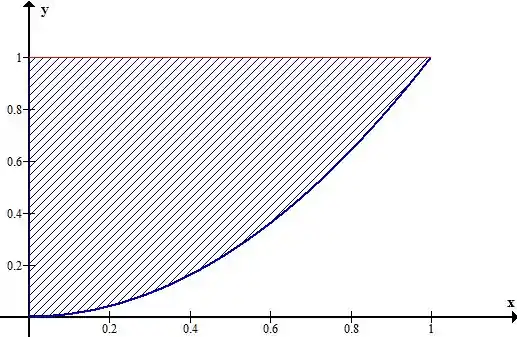
Invertendo a ordem de integração:
Como temos que é positivo, vamos pegar somente a raiz positiva
Os limites de continuam os mesmos:
Passo 3
Reescrevendo a integral:
Passo 4
Integrando em :
Para integrar em , vamos fazer a substituição
Os limites em ficam:
Temos então a integral:
Integrando em :
Integrando em :
Resposta
Exercício Resolvido #3
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009
Calcule a integral mudando a ordem de integração de forma apropriada
Passo 1
Vemos que o problema nessa integral não é a primeira integração, em , mas sim depois para integrar em , portanto vamos ter que mudar a ordem de integração, mas vamos manter a primeira integral em , vai ficar então .
Olhando os limites dados pela integral, vemos que o nosso sólido é definido por:
Nosso esboço fica:
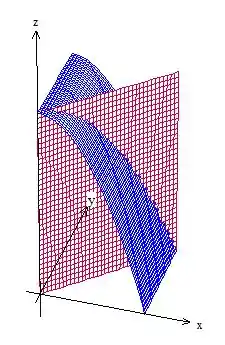
Passo 2
Como vamos manter a primeira integração em , podemos analisar somente o plano , nele tínhamos limitado por
E limitado por
No gráfico temos:
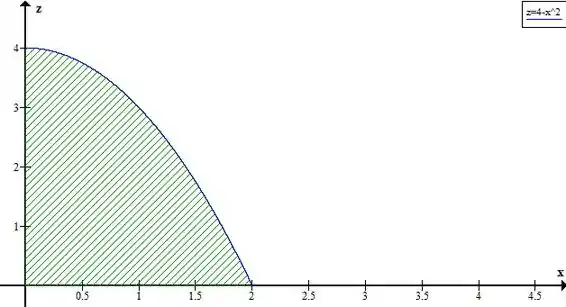
Invertendo a ordem de integração:
Como temos positivo, vamos somente considerar a raiz positiva:
Como não foi alterado, seus limites continuam
Passo 3
Colocando tudo na integral mudada, temos:
Passo 4
Integrando em
Integrando em
Integrando em