Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integrais Triplas - Regiões Gerais

Ver Todos os Exercícios

Teoria

Fala ai, bem vindo ao RespondeAi! Vamos falar de integrais triplas, para iniciar nossos entendimentos de problemas de integrais triplas, primeira vamos definir três tipos de regiões que podem existir para aplicar nossa integral:

Região do Tipo I

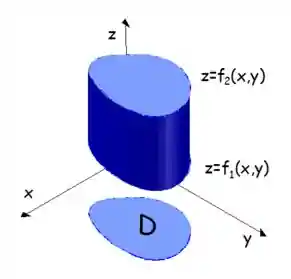
Para esse tipo de região a variável varia entre duas funções e são limitadas no plano por um sólido de área :

Para calcular o volume desse sólido que tem essa projeção no plano , poderíamos descrever a região da seguinte forma:

Região do Tipo II

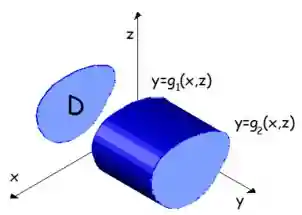
Para esse tipo de região a variável varia entre duas funções e são limitadas no plano por um sólido de área :

Para calcular o volume desse sólido que tem essa projeção no plano , poderíamos descrever a região da seguinte forma:

Região do Tipo III

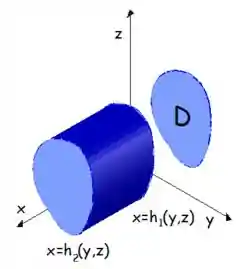
Por último para esse tipo de região a variável varia entre duas funções e são limitadas no plano por um sólido de área :

Para calcular o volume desse sólido que tem essa projeção no plano , poderíamos descrever a região da seguinte forma:

E como não temos nenhuma função com três variáveis, para resolver questões de integrais triplas, teremos que fazer um integral simples e um integral dupla, vamos ver um exemplo.

Supondo que tivéssemos um exercício do tipo III a seguinte integral tripla que teríamos que resolver serie:

Vamos ver um exemplo para entender tudo direitinho!

Vamos pensar no seguinte exemplo, sabendo que existe um sólido dentro do cilindro , delimitado por e . Calcule:

Passo 1

Para começar a resolver esse problema de integrais triplas primeiro precisaremos entender de que tipo de região estamos tratando, fazendo um esboço dessas funções poderíamos encontrar um gráfico com essa cara aqui:

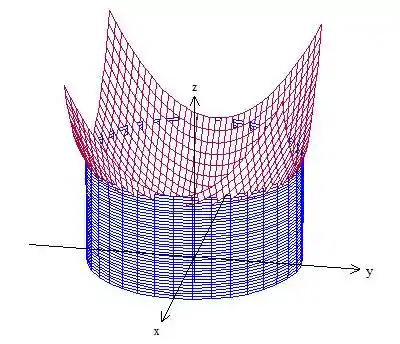
Temos um cilindro limitado por baixo pelo plano e por cima por um paraboloide,

Além do gráfico no ajudar, podemos perceber pelo enunciado que estamos trabalhando com uma região do tipo I já que temos um sólido limitado por duas funções , e sabemos que .

Passo 2

Nossa região passa a ser descrita da seguinte forma:

Passo 3

Nossa integral fica

Passo 4

Para resolver essa integral iremos fazer como fazíamos muitas vezes para calcular integrais duplas e mudar nossas coordenadas cartesianas para coordenadas polares, e vamos fazer isso porque se olharmos nossa projeção do nosso sólido no plano vemos um círculo:

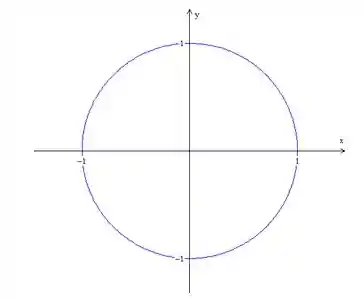
Por isso que coordenadas polares podem nos ajudar!

📢 OBS: Para qualquer tipo de região, depois que escolhermos os limites da primeira integral, vamos cair em uma integral dupla, e para resolvê-la vamos usar os métodos já conhecidos para a resolução de integrais duplas.

Para mudar para coordenadas polares temos que nos lembrar que:

E não podemos esquecer do nosso Jacobiano, mas por ser tratar de um círculo, podemos afirmar que:

Onde vamos iterar entre:

Passo 5

Voltando para nossa integral:

Resolvendo todas essas integrais iteradas:

Legal né? No nosso site você encontra uma série de exercícios resolvidos sobre Integrais Triplas, e aprende tudo que você precisa para mandar bem em Cálculo!

Exercício

Para não ficar perdido no assunto confere aqui em baixo um de nossos exercício do tópico de Integrais Triplas em Regiões Gerais, feito por um de nossos Experts especialmente para você, com nosso método de resolução Passo a Passo!

Calcule o volume do sólido limitado pelo cone e o paraboloide .

Região do Tipo III

Exercício

Exercícios Resolvidos

Exercício Resolvido #1

CEFET - Cálculo 2 - P1 Roberto Sa 2012.1 – 2

Considere a região no primeiro octante delimitada pelo plano x + y = 1 e pelo paraboloide z = 4 - x 2 - y 2 .

  1. Descreva a região delimitada.
  2. Calcule o volume dessa região.

Passo 1

Letra a)

Bem, vamos começar desenhando essa região ai, para entender melhor o problema. Temos um paraboloide z = 4 - x 2 - y 2 virado para baixo (em vermelho), limitado ao primeiro octante (planos em verde) e cortado pelo plano x + y = 1 (em azul).

Para você visualizar melhor, a região é essa aqui:

Beleza?

Passo 2

Como podemos ver, no plano x y , temos um domínio D . Em z , o sólido é limitado embaixo pelo plano z = 0 e em cima pelo outro plano paraboloide. Vamos, então, escrever essa região como tipo I.

Temos a coordenada z variando desde z = 0 até a superfície do paraboloide z = 4 - x 2 - y 2 , logo, 0 ≤ z ≤ 4 - x 2 - y 2 . Logo, a região pode ser escrita como:

W = { ( x , y , z ) | x , y ∈ D ;   0 ≤ z ≤ 4 - x 2 - y 2 }

Passo 3

Vendo a região de cima, podemos descobrir seu domínio D , que, no caso, é o seguinte triângulo:

Essa reta azul é onde o plano x + y = 1 corta o plano z = 0 . Portanto, sua equação é a própria equação do plano fazendo z = 0 , y = 1 - x .

Podemos dizer, então, que y varia desde y = 0 até a equação da reta y = 1 - x , enquanto x varia desde x = 0 até x = 1 .

Temos, então:

D = ( x , y | 0 ≤ x ≤ 1 ; 0 ≤ y ≤ 1 - x }

Portanto,

W = { ( x , y , z ) | 0 ≤ x ≤ 1 ; 0 ≤ y ≤ 1 - x , 0 ≤ z ≤ 4 - x 2 - y 2 }

Passo 4

Letra b)

Bom, o volume desse sólido será V = ∫ d V = ∭ w   d x d y d z , certo?

Vamos agora substituir os intervalos que encontramos na integral iterada:

∭ w   d x d y d z = ∫ 0 1   ∫ 0 1 - x   ∫ 0 4 - x 2 - y 2 d z d y d x

Cuidado com a ordem dos diferenciais! Ela tem que obedecer a ordem dos intervalos nas integrais. Lembre-se de que o último intervalo (o de fora) dever ser sempre um número.

Passo 5

Integrando em relação a z , temos:

= ∫ 0 1   ∫ 0 1 - x   z z = 0 z = 4 - x 2 - y 2 d y d x = ∫ 0 1   ∫ 0 1 - x 4 - x 2 - y 2 d y d x

Passo 6

Agora, integramos em relação a y :

= ∫ 0 1   4 y - x 2 y - y 3 3 0 1 - x d x =

= ∫ 0 1   4 - 4 x - x 2 + x 3 - 1 - 3 x + 3 x 2 - x 3 3 d x =

= ∫ 0 1 11 3 - 3 x - 2 x 2 + 4 x 3 3 d x =

Passo 7

Finamente, integramos em relação a x :

= 11 x 3 - 3 x 2 2 - 2 x 3 3 + x 4 3 0 1 =

= 11 3 - 3 2 - 2 3 + 1 3 =

= 11 6

Resposta

a )       W = { ( x , y , z ) | 0 ≤ x ≤ 1 ; 0 ≤ y ≤ 1 - x , 0 ≤ z ≤ 4 - x 2 - y 2 }

b )       11 6

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 205

Calcule o volume do sólido W limitado pelo cone z = x 2 + y 2 e o paraboloide z = x 2 + y 2 .

Passo 1

Bom, o volume desse sólido será V = ∫ d V = ∭ w   d x d y d z , certo? Agora precisamos descrever a região de integração W . Vamos começar fazendo um esboço dela:

A superfície azul é o paraboloide (virado para cima porque temos x 2 e y 2 multiplicados por termos positivos), e a vermelha, a folha superior do cone (pois não podemos ter raiz negativa).

Como podemos ver, no plano x y , temos um domínio D . Em z , o sólido é limitado embaixo pelo paraboloide z = x 2 + y 2 e em cima pelo cone z = x 2 + y 2 . Vamos, então, escrever essa região como tipo I:

W = { ( x , y , z ) | x , y ∈ D ;   x 2 + y 2 ≤ z ≤ x 2 + y 2 }

Passo 2

Agora precisamos descrever o domínio D . Para isso, faremos um esboço da projeção do sólido plano x y :

Fazendo a interseção da equação do cone com a equação do paraboloide, temos:

z = z 2   → z = 0   ou   z = 1

Em z = 0 , as superfícies se encontram, pois ambas partem da origem. Em z = 1 temos uma circunferência de raio 1. Então, se a projetarmos no plano x y , teremos a figura acima. Se substituirmos esse valor nas equações das superfícies, encontramos, de fato, x 2 + y 2 = 1 .

Como se trata de uma circunferência, vamos escrevê-la com coordenadas polares:

D = ( x , y | 0 ≤ r ≤ 1 ; 0 ≤ θ ≤ 2 π }

Passo 3

Vamos agora substituir os intervalos que encontramos:

∬ D   ∫ x 2 + y 2 x 2 + y 2 d z d A

Deixamos para escrever os intervalos de D depois para não gerar confusão, pois teremos que fazer a mudança para coordenadas polares.

Passo 4

Integrando em relação a z , temos:

= ∬ D   z x 2 + y 2 x 2 + y 2 d A =

= ∬ D   x 2 + y 2 - x 2 - y 2 d A =

Passo 5

Agora vamos descrever a região D fazendo a mudança para coordenadas polares (não se esqueça do Jacobiano!). Lembre-se também de que x 2 + y 2 = r 2 .

= ∫ 0 2 π ∫ 0 1 r 2 - r 2 r d r d θ =

= ∫ 0 2 π ∫ 0 1 r 2 - r 3 d r d θ =

Passo 6

Integrando em relação a r :

= ∫ 0 2 π r 3 3 - r 4 4 r = 0 r = 1 d θ =

= 1 12 ∫ 0 2 π d θ =

Passo 7

Finamente, integramos em relação a θ :

= θ 12 0 2 π =

= 2 π 12 =

Resposta

π 6

Exercício Resolvido #3

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 944

Calcule ∭ E   x 2 + z 2 d V , onde E é a região limitada pelo paraboloide y = x 2 + z 2 e pelo plano y = 4 .

Passo 1

Vamos fazer um esboço dessa região E :

Temos o paraboloide “virado de lado” porque o eixo de simetria é o y (o termo que não está elevado ao quadrado).

Como y varia entre a equação do paraboloide e y = 4 e temos, no plano x z , uma projeção do sólido que representa um domínio D (um círculo), vamos descrever essa região como tipo II.

W = { ( x , y , z ) | x , z ∈ D ;   x 2 + z 2 ≤ y ≤ 4 }

Passo 2

Perceba que o paraboloide é formado por várias circunferências paralelas a x z , que vão aumentando quando y aumenta. A projeção no plano x z vai ser exatamente a maior dessas circunferências, onde o paraboloide corta o plano y = 4 . Substituindo esse valor na sua equação, temos então a seguinte circunferência: x 2 + z 2 = 4 .

A melhor forma de descrever essa área, como já vimos, é por meio de coordenadas polares, fazendo:

x = r cos ⁡ θ  

z = r sen ⁡ θ

| J | = r

Teremos:

D = ( r , θ | 0 ≤ θ ≤ 2 π ; 0 ≤ r ≤ 2 }

Passo 3

Vamos agora substituir os intervalos que encontramos para a integral iterada. Como tivemos que fazer uma mudança de variáveis para descrever o domínio D , vamos escrevê-lo depois da primeira integração, para não gerar confusões. Temos:

∬ D     ∫ x 2 + z 2 4 x 2 + z 2 d y d A =

Passo 4

Integrando em relação a y , temos:

= ∬ D     y x 2 + z 2 y = x 2 + z 2 y = 4 d A =

= ∬ D   x 2 + z 2   ( 4 - x 2 - z 2 ) d A =

Passo 5

Agora sim, vamos substituir os intervalos de D e fazer a substituição polar (Não se esqueça do Jacobiano!).

Você poderia ter feito isso antes, sem problemas. Optamos por fazer assim apenas por questão de organização.

= ∫ 0 2 π   ∫ 0 2 r cos ⁡ θ 2 + ( r sen ⁡ θ )   2   ( 4 - r cos ⁡ θ 2 - r sen ⁡ θ )   2 r   d r d θ =

= ∫ 0 2 π   ∫ 0 2   r ( 4 - r 2 ) r   d r d θ =

= ∫ 0 2 π   ∫ 0 2 4 r 2 - r 4   d r d θ =

- ''

Passo 6

Agora, integramos em relação a r :

= ∫ 0 2 π 4 r 3 3 - r 5 5 r = 0 r = 2 d θ =

= ∫ 0 2 π 32 3 - 32 5   d θ = ∫ 0 2 π 64 15   d θ =

Passo 7

Finamente, integramos em relação a θ :

= 64   θ 15 0 2 π =

Resposta

128 π 15

Exercício Resolvido #4

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 948

Use a integral tripla para determinar o volume do sólido delimitado pelo cilindro x = y 2   e pelos planos z = 0 e x + z = 1 .

Passo 1

Bom, o volume desse sólido será V = ∫ d V = ∭ w   d x d y d z , certo? Agora precisamos descrever a região de integração W . Vamos começar fazendo um esboço dela:

A superfície vermelha representa a equação x = y 2 , que é independente de z (ou seja, é a equação de um cilindro), por isso, temos várias parábolas “alinhadas” ao longo desse eixo. O plano azul x + z = 1 tem equação independente de y , então pode ser interpretado como várias retas x + z = 1 ao longo desse eixo.

Como podemos ver, no plano x y , temos um domínio D . Em z , o sólido é limitado embaixo pelo plano z = 0 e em cima pelo outro plano z = 1 - x . Vamos, então, escrever essa região como tipo I:

W = { ( x , y , z ) | x , y ∈ D ;   0 ≤ z ≤ 1 - x }

Passo 2

Agora precisamos descrever o domínio D . Para isso, faremos um esboço da projeção do sólido plano x y :

Fazendo a interseção da equação do cilindro e da equação do plano x + z = 1 com z = 0 , descobrimos as equações dessas curvas acima, que serão x = y 2 e x = 1 .

Vamos descrever essa área como tipo II (poderíamos ter descrito como tipo I também), pois temos o intervalo de y entre dois números e o de x entre a função da parábola (em vermelho) e a da reta (em azul). Substituindo x = 1 na equação da parábola, vemos que y varia entre - 1 e 1 . Temos, então:

D = ( x , y | - 1 ≤ y ≤ 1 ; y 2 ≤ x ≤ 1 }

Passo 3

Vamos agora substituir os intervalos que encontramos na integral iterada:

∫ - 1 1   ∫ y 2 1   ∫ 0 1 - x d z d x d y =

Passo 4

Integrando em relação a z , temos:

= ∫ - 1 1   ∫ y 2 1   z z = 0 z = 1 - x d x d y = ∫ - 1 1   ∫ y 2 1   1 - x d x d y =

Passo 5

Agora, integramos em relação a x :

= ∫ - 1 1   x - x 2 2 x = y 2 x = 1 d y = ∫ - 1 1   1 - 1 2 - y 2 - y 4 2 d y = ∫ - 1 1 1 2 - y 2 + y 4 2 d y =

Passo 6

Finamente, integramos em relação a y :

= y 2 - y 3 3 + y 5 10 - 1 1 = 1 2 - 1 3 + 1 10 — - 1 2 + 1 3 - 1 10 =

Resposta

8 15

Exercício Resolvido #5

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 195

Calcule o volume do sólido W limitado pelas superfícies de equações z + x 2 = 9 , y + z = 4 , y = 0 e y = 4 .

Passo 1

O volume pedido será dado por ∭ W   d x d y d z . Vamos fazer um esboço dessa região W :

A superfície vermelha representa o cilindro de equação z + x 2 = 9 , independente de y . Assim, podemos interpretar como várias parábolas z = 9 - x 2 ao longo desse eixo. Podemos utilizar o mesmo raciocínio para o plano azul, de equação y + z = 4 , independente de x .

Como podemos ver a variável z varia entre o plano z = 4 - y e o cilindro parabólico z = 9 - x 2 . No plano x y , a projeção do sólido representa um domínio D . Vamos escrever, então, essa região como tipo I:

W = { ( x , y , z ) | x , y ∈ D ;   4 - y ≤ z ≤ 9 - x 2 }

Passo 2

Agora precisamos descrever o domínio D . Para sabermos que região é essa, vamos fazer a interseção entre o cilindro e plano inclinado:

z = 9 - x 2 = 4 - y

y = x 2 - 5

z = 9 - x 2 z = 4 - y → 9 - x 2 = 4 - y ∴ y = x 2 - 5

A projeção da interseção no plano x y é, portanto, uma parábola de concavidade para cima. Podemos, agora, fazer um esboço dessa região:

Para descobrirmos a equação dessa reta vermelha basta fazer a interseção do plano inclinado com o plano x y , ou seja, substituindo z = 0 em z = 4 - y teremos y = 4 .

Como a região está limitada na esquerda e na direita pela parábola e em cima e embaixo por uma constante, vamos escrevê-la como tipo II. Já sabemos que y varia entre 0 e 4 . Isolando os termos x na equação da parábola, temos ± y + 5 , então, escrevemos a região como:

D = ( x , y | 0 ≤ y ≤ 4 ; - y + 5 ≤ x ≤ y + 5 }

Passo 3

Vamos agora substituir os intervalos que encontramos para a integral iterada:

∫ 0 4   ∫ - y + 5 y + 5   ∫   4 - y 9 - x 2 d z d x d y =

Passo 4

Vamos começar integrando em relação a z

= ∫ 0 4   ∫ – y + 5 y + 5 z   z = 4 - y z = 9 - x 2   d x d y =

= ∫ 0 4   ∫ – y + 5 y + 5 ( 9 - x 2 - 4 + y )   d x d y = ∫ 0 4   ∫ – y + 5 y + 5 ( 5 - x 2 + y )   d x d y =

Passo 5

Agora integraremos em relação a x :

= ∫ 0 4 5 x - x 3 3 + x y x = – y + 5 x = y + 5   d y =

= ∫ 0 4 y + 5 1 / 2 5 + y - y + 5 3 / 2 3   - - y + 5 1 / 2 5 + y + y + 5 3 / 2 3   d y =

= ∫ 0 4 2 y + 5 3 / 2 - 2 y + 5 3 / 2 3   d y =

Passo 6

Finamente, integramos em relação a y :

= 2 . 2 5 y + 5 5 / 2 - 2 3 . 2 5 y + 5 5 / 2 0 4 =

= 8 15 y + 5 5 / 2 0 4 =

Resposta

8 15 243 - 25 5

Exercício Resolvido #6

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 949, adaptado.

Sendo E o sólido limitado pelo cilindro y 2 + z 2 = 9 e pelos planos x = 0 , y = 3 x e z = 0 no primeiro octante, com função densidade ρ x , y , z = x 2 + y 2 , determine sua massa

Passo 1

O problema pede que calculemos a massa do sólido delimitado pelas superfícies acima, sabendo que sua densidade é dada por ρ x , y , z . Nós sabemos que:

d m = ρ x , y , z d V

Onde d m é o diferencial de massa e d V o de volume. Integrando ambos os lados na região E em que o sólido está contido, temos que:

M = ∭ E   ρ x , y , z d V

M = ∭ E   ( x 2 + y 2 )   d x d y d z

Vamos fazer um esboço dessa região E :

Fazendo os cortes no primeiro octante, temos isso aqui:

Como x varia entre a equação dos planos x = 0 e x = y 3 e temos, no plano y z , uma projeção do sólido que representa um domínio D (um setor de círculo), vamos descrever essa região como tipo III.

W = x , y , z y , z ∈ D ;   0 ≤ x ≤ y 3

Passo 2

A projeção do sólido no plano y z é esse setor aqui:

Com raio r = 3 , porque o cilindro possui raio 3 .

A melhor forma de descrever essa área, é por meio de coordenadas polares, fazendo:

y = r cos ⁡ θ  

z = r sen ⁡ θ

| J | = r

Teremos:

D = r , θ 0 ≤ θ ≤ π 2 ; 0 ≤ r ≤ 3

Passo 3

Vamos agora substituir os intervalos que encontramos nas integrais iteradas. Como tivemos que fazer uma mudança de variáveis para descrever o domínio D , vamos escrevê-lo depois da primeira integração, para não gerar confusões. Temos:

M = ∭ E   ( x 2 + y 2 )   d x d y d z = ∬ D     ∫ 0 y / 3   ( x 2 + y 2 )   d x d A

Passo 4

Integrando em relação a x , temos:

= ∬ D     x 3 3 + x y 2 0 y / 3 d A =

= ∬ D   y 3 81 + y 3 3 d A =

= 28 81 ∬ D   y 3 d A =

Passo 5

Agora sim, vamos substituir os intervalos de D e fazer a substituição polar.

Você poderia ter feito isso antes, sem problemas. Optamos por fazer assim apenas por questão de organização.

= 28 81 ∫ 0 π / 2   ∫ 0 3   r 3 cos 3 ⁡ θ   r   d r d θ =

= 28 81 ∫ 0 π / 2   ∫ 0 3   cos 3 ⁡ θ   r 4   d r d θ =

Passo 6

Agora, integramos em relação a r :

= 28 81 × 5 ∫ 0 π / 2 cos 3 ⁡ θ r 5 r = 0 r = 3 d θ =

= 84 5 ∫ 0 π / 2 cos 3 ⁡ θ d θ =

Passo 7

Agora, nós fazemos o seguinte:

= 84 5 ∫ 0 π / 2 cos ⁡ θ cos 2 ⁡ θ   d θ =

= 84 5 ∫ 0 π / 2 cos ⁡ θ 1 - sen 2 ⁡ θ d θ =

= 84 5 ∫ 0 π / 2 cos ⁡ θ   d θ - 84 5 ∫ 0 π / 2 cos ⁡ θ sen 2 ⁡ θ d θ =

= 84 5 sen ⁡ θ 0 π / 2 - 84 5 ∫ 0 π / 2 cos ⁡ θ sen 2 ⁡ θ d θ =

= 84 5 1 - 0 - 84 5 ∫ 0 π / 2 cos ⁡ θ sen 2 ⁡ θ d θ =

= 84 5 - 84 5 ∫ 0 π / 2 cos ⁡ θ sen 2 ⁡ θ d θ =

Então, vamos a substituição

sen ⁡ θ = u

cos ⁡ θ   d θ = d u

θ = 0           →           u = 0

θ = π 2           →           u = 1

Aplicando na integral

= 84 5 - 84 5 ∫ 0 1 u 2 d u =

= 84 5 - 84 5 u 3 3 0 1 =

= 84 - 28 5 = 56 5

Resposta

56 5

Exercícios de Livros Relacionados

Escrever na forma de uma integral tripla iterada: ∫ ∫ ∫ T f d V Onde T é delimitada por x 2 + z 2 = a 2 ,y 2 + z 2 = a 2
Esboçar a região de integração e calcular as integrais ∫ 0 1 ∫ x 2 x ∫ 0 2 + x + y x d z d y d x
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Calcule a integral iterada. ∫ 0 3 ∫ 0 1 ∫ 0 1 - z 2 z e yd xd zd y
Calcule a integral iterada.int_0^(sqrt(pi)) int_0^x int_0^(x z) x^2 s e n y d y d z d x