Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integrais Impróprias – Limites Sendo Infinito

Ver Todos os Exercícios

Teoria

O que são integrais impróprias?

Eai, galeeera! Tudo tranquilo?

Pergunta rápida, o que você faria se eu pedisse para você resolver essa integral aqui:

∫ 1 5 1 x 2 d x

Mamão com açúcar, né?

E se ao invés dessa integral, eu te pedisse para você resolver essa daqui:

∫ 1 ∞ 1 x 2 d x

Parece que o nosso mamão está mais para um jiló, né?

Bem, isso é o que chamamos de integral imprópria e, como o título ali em cima já deu um spoiler legal, esse tipo de integralzinha vai ser resolvida por meio de limites.

Tá, mas como podemos identificar esse tipo de integral?

Fica tranquilo! Elas são bem fáceis de identificar e se resumem a basicamente dois tipos, mas nesse tópico iremos focar em quando pelo menos um dos limites de integração é infinito, quando isso acontece você vai se deparar com algo desse tipo:

∫ a ∞ f x d x

Sim, é isso mesmo, em vez de termos um intervalo [ a ,   b ] bonitinho, agora temos um infinito no meio desse rolê.

∫ a b f x d x

Sem neurose, vamos aprender como a resolver essas belezinhas.

Um dos limites de integração no infinito

Beleza, agora que já sabemos que estamos falando sobre integrais impróprias, vamos voltar naquela integral que eu te mostrei no início, essa daqui:

∫ 1 ∞ 1 x 2   d x

Como podemos resolvê-la?

Simples! Vou te mostrar um passo a passo que vai sair que nem mágica.

1º Passo: substitua o infinito presente no intervalo da integral por uma variável, nesse caso iremos usar t .

∫ 1 t 1 x 2   d x

2º Passo: faça com que a integral seja a função de um limite que tenha a variável que você escolheu, nesse caso t , tendendo ao infinito da função.

lim t → ∞ ⁡ ∫ 1 t 1 x 2   d x

3º Passo: resolva a integral e aplique os limites de integração.

lim t → ∞ ⁡ ∫ 1 t 1 x 2   d x

= lim t → ∞ ⁡ ∫ 1 t x - 2   d x

= lim t → ∞ ⁡ x - 1 - 1 1 t = t - 1 - 1 - 1 - 1 - 1

= 1 t × 1 - 1 - 1 1 × 1 - 1 = [ - 1 t - ( - 1 1 ) ]

= [ - 1 t + 1 ]

4º Passo: resolva o limite.

lim t → ∞ ⁡ - 1 t + 1 = - 0 + 1 = 1

Prontinho! A área que calculamos, foi essa daqui:

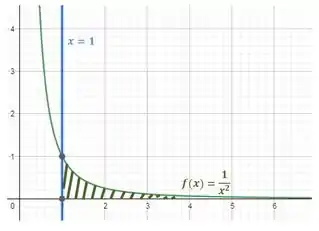
Também podemos ter casos no intervalo de integração de - ∞ , como nessa integral:

∫ - ∞ 0 x e x d x

Basta seguirmos novamente aquele passo a passo que é sucesso.

1º Passo: Substitua o seu infinito por uma letra qualquer, agora iremos usar A .

∫ A 0 x e x d x

2º Passo: Jogue a integral dentro de um limite, fazendo a letra que você escolheu tender ao infinito.

lim A → - ∞ ⁡ ∫ A 0 x e x d x

Observe que dessa vez temos - ∞ . Portanto, cuidado com o sinal!

3º Passo: Resolva a integral e depois passe o limite.

Resolvendo a integral por partes, u = x e v ' = e x :

∫ A 0 x e x d x = x e x A 0 - ∫ A 0 e x d x = e x ( x - 1 ) A 0

Aplicando os limites de integração:

e x ( x - 1 ) A 0 = e 0 0 - 1 - e A A - 1 = e A - A e A - 1

Agora, vamos resolver o limite:

lim A → - ∞ ⁡ ∫ A 0 x e x d x = lim A → - ∞ ⁡ e A - A e A - 1

Quando A assume valores grandes e negativos, passamos a ter expoentes negativos, que inverte a fração e tende a 0.

lim A → - ∞ ⁡ e A - A e A - 1 = lim A → ∞ ⁡ 1 e A - A e A - 1 = - 1

Só mais uma coisinha, nos dois casos, podemos analisar a convergência da integral:

  • se o limite existir, isto é, for um número finito, dizemos que essa integral é convergente
  • se ao calcular o limite encontrarmos ± ∞ , dizemos que a integral é divergente

Por exemplo, vejamos se essa integral imprópria é convergente:

∫ - ∞ 3 1 - x + 5 2 d x

Temos uma integral imprópria com limite de integração inferior - ∞ , então fazemos:

1º Passo: Substitua o seu infinito por uma letra qualquer, novamente vamos usar A .

∫ A 3 1 - x + 5 2 d x

2º Passo: Jogue a integral dentro de um limite, fazendo a letra que você escolheu tender ao infinito.

Assim, temos:

∫ - ∞ 3 1 - x + 5 2 d x = l i m A → - ∞ ∫ A 3 1 - x + 5 2   d x

3º Passo: Resolva a integral e depois passe o limite.

A integral indefinida é:

∫ 1 - x + 5 2 d x = 1 - x + 5 + C

(Não vou entrar em detalhes aqui, mas é tranquilo de calcular, basta usar a substituição u = - x + 5 ).

Aplicando os limites de integração:

1 - x + 5 A 3 = 1 - 3 + 5 - 1 - A + 5 = [ 1 2 - 1 5 - A ]

Agora é só aplicar o limite:

l i m A → - ∞ ∫ A 3 1 - x + 5 2   d x = l i m A → - ∞ 1 2 - 1 5 - A = 1 2

Como obtemos como resultado um número finito, dizemos que essa integral é convergente.

Dois Limites Sendo Infinito

Show, já aprendemos a lidar com um dos limites de integração indo para o infinito, mas e se temos os dois?

∫ - ∞ + ∞ f x d x

Não tem muito mistério, é só abrir em duas juntando as que vimos antes:

∫ - ∞ ∞ f x d x = ∫ - ∞ c f x d x +   ∫ c ∞ f x d x

Onde c é uma constante qualquer, geralmente escolhemos usar o 0.

Vejamos logo um exemplo: vamos determinar se a área da região hachurada na figura aqui embaixo pode ser representada por um número finito.

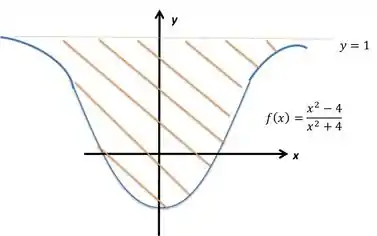
Observe que y = 1 é uma assíntota horizontal.

Nesse caso, a área da região é dada por:

A =   ∫ - ∞ + ∞ 1 - f x d x

Ou seja, queremos saber se essa integral aí em cima é convergente ou divergente.

Usando a definição, vamos abrir como a soma de duas:

∫ - ∞ ∞ 1 - f x d x = ∫ - ∞ c 1 - f x d x +   ∫ c ∞ 1 - f x d x

Vamos usar nosso passo a passo:

1º Passo: Substitua o seu infinito por uma letra qualquer, vamos usar A para primeira integral e B para segunda.

2º Passo: Jogue a integral dentro de um limite, fazendo a letra que você escolheu tender ao infinito.

Assim, temos:

lim A → - ∞ ⁡ ∫ A c 1 - f x d x + lim B → ∞ ⁡ ∫ c B 1 - f x d x  

3º Passo: Resolva a integral, e depois passe o limite.

Para resolver, primeiro calculamos a integral indefinida:

∫ 1 - f x d x = ∫ 1 - x 2 - 4 x 2 + 4 d x

= ∫ x 2 + 4 - ( x 2 - 4 ) x 2 + 4 d x = ∫ 8 x 2 + 4 d x

⇒ ∫ 1 - f x d x = 4 arctg ⁡ x 2 + C

Aplicando os limites de integração:

∫ - ∞ c 1 - f x d x = lim A → - ∞ ⁡ 4 arctg ⁡ x 2 A c

= lim a → - ∞ ⁡ 4 arctg ⁡ c 2 - 4 arctg ⁡ A 2

Da mesma forma, temos:

∫ c + ∞ 1 - f x d x = l i m B → + ∞ 4 arctg ⁡ x 2 c B

= l i m B → + ∞ 4 arctg ⁡ B 2 - 4 arctg ⁡ c 2

Resolvendo o limite:

l i m A → - ∞ 4 arctg ⁡ c 2 - 4 arctg ⁡ A 2 = 4 arctg ⁡ c 2 + 4 π 2

l i m B → + ∞ 4 arctg ⁡ B 2 - 4 arctg ⁡ c 2 = 4 π 2 - 4 arctg ⁡ c 2

Vale lembrar que:

lim x → ± ∞ ⁡ arctg ⁡ x = ± π 2

Enfim, voltando pra nossa integral imprópria:

∫ - ∞ ∞ 1 - f x d x = ∫ - ∞ c 1 - f x d x +   ∫ c ∞ 1 - f x d x

∫ - ∞ ∞ 1 - f x d x = 4 arctg ⁡ c 2 + 4 π 2 + 4 π 2 - 4 arctg ⁡ c 2

∫ - ∞ ∞ 1 - f x d x = 4 π  

O resultado da integral é um número finito. Logo, a área da região R pode ser representada por um número finito! Em outras palavras, a integral é convergente!

Revisãozinha

Agora pega seu papelzinho e caneta e anota isso aqui essa revisão maneiríssima.

Temos dois tipos de integrais impróprias:

  • Intervalos infinitos;
  • Descontinuidade em um ponto do intervalo (abordado em outro tópico).

Depois de resolver elas, podemos dizer que elas são:

  • Convergente: se o limite existe como um número finito;
  • Divergente: se encontrarmos ± ∞

Para resolvermos uma integral imprópria, no caso de intervalos infinitos, usamos três passos, são eles:

1º Passo: Substitua o seu infinito por uma letra qualquer;

2º Passo: Jogue a integral dentro de um limite, fazendo a letra que você escolheu tender ao infinito;

3º Passo: Resolva a integral e depois resolva o limite.

Dois Limites Sendo Infinito

Revisãozinha

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Calcule:

∫ 2 ∞ 1 x ln ⁡ x d x

Passo 1

Visto que um dos limites de integração é infinito, concluímos que se trata de uma integral imprópria! E portanto devemos escrever:

∫ 2 ∞ 1 x ln ⁡ x d x = lim t → ∞ ⁡ ∫ 2 t 1 x ln ⁡ x d x

Passo 2

E pra resolver a integral indefinida

∫ 1 x ln ⁡ x d x

vamos ter que fazer a substituição

u = ln ⁡ x ⇒ d u = 1 x d x

A integral então ficará:

∫ 1 u d u = ln ⁡ u + C = ln ⁡ ( ln ⁡ x ) + C

Passo 3

Voltando na integral imprópria:

∫ 2 ∞ 1 x ln ⁡ x d x = lim t → ∞ ⁡ ∫ 2 t 1 x ln ⁡ x d x

= lim t → ∞ ⁡ ln ⁡ ( ln ⁡ t ) - ln ⁡ ( ln ⁡ 2 ) = ∞

Deu infinito, então a integral diverge!

Resposta

A integral diverge.

Exercício Resolvido #2

UFF - Cálculo IIA - P1 Marlene 2014.2 - 4b

Analise a convergência da integral imprópria

∫ 1 ∞ 1 x 4 sen ⁡ 1 x d x

Passo 1

Temos uma integral imprópria, pois um dos limites de integração é infinito. A função 1 x 4 s e n   1 x é contínua no intervalo de integração [ 1 , + ∞ ) dado, então tá sussa!

Ele pede para analisarmos a convergência. Basicamente, vamos calcular o limite dessa integral e ver se o limite dá um número finito. Se sim, então a integral é convergente. Se ao calcular o limite obtivermos um valor do tipo ± ∞ , a integral é divergente. Vamos seguir o barco?

Passo 2

Já sabemos que quando temos uma integral imprópria com limite superior ∞ , fazemos isso aqui:

∫ a ∞ f x d x = lim b → ∞ ⁡ ∫ a b f x d x

Então:

∫ 1 ∞ 1 x 4 sen ⁡ 1 x d x = lim b → ∞ ⁡ ∫ 1 b 1 x 4 sen ⁡ 1 x d x

Para resolver, eu vou achar a primitiva

∫ 1 x 4 sen ⁡ 1 x d x

E depois aplicar o Teorema Fundamental do Cálculo – Parte 2 e então calcular o limite. Para calcular a primitiva, a primeira coisa que vou fazer é uma substituição para facilitar a vida. Acompanha aqui.

t = 1 x → d t =   - 1 x 2 d x

E é ai que entre a mágica! Veja só, podemos chamar:

1 x 4 =   - 1 x 2 - 1 x 2

- 1 x 2 = - 1 x 1 x = - t 2

Aplicando essas igualdades na integral, chegamos à:

∫ 1 x 4 sen ⁡ 1 x d x = ∫ - 1 x 2 - 1 x 2 sen ⁡ 1 x d x = ∫ - 1 x 2 sen ⁡ 1 x   - 1 x 2 d x

∫ 1 x 4 sen ⁡ 1 x d x = ∫ -   t 2 sen ⁡ t   d t

Passo 3

E agora? Essa integral sai por partes, concorda?

∫ - t 2 s e n   t   d t  

Pela nossa regrinha do LIATE, eu devo chamar de u o polinômio t 2 e de d v a função trigonométrica s e n   t   d t

u = - t 2 → d u = - 2 t   d t

d v = s e n   t   d t → v = ∫ s e n   t   d t → v = - cos ⁡ t

Como a integração por partes segue o modelo:

∫ u   d v   = u v - ∫ v   d u  

Vamos ter:

∫ - t 2 s e n   t   d t   = - t 2 - cos ⁡ t - ∫ - cos ⁡ t   - 2 t   d t  

∫ - t 2 s e n   t   d t   = t 2 cos ⁡ t - ∫ 2 t cos ⁡ t   d t  

Passo 4

A integral ∫ 2 t cos ⁡ t   d t   é resolvida aplicando-se partes novamente:

u = 2 t → d u = 2   d t

d v = cos ⁡ t   d t → v = ∫ c o s   t   d t → v = s e n   t

Como a integração por partes segue o modelo:

∫ u   d v   = u v - ∫ v   d u  

Vamos ter:

∫ 2 t cos ⁡ t   d t   = 2 t sin ⁡ t - ∫ 2 sin ⁡ t   d t  

∫ 2 t cos ⁡ t   d t   = 2 t sin ⁡ t + 2 cos ⁡ t

Passo 5

Substituindo:

∫ - t 2 s e n   t   d t   = t 2 cos ⁡ t - ∫ 2 t cos ⁡ t   d t  

∫ 2 t cos ⁡ t   d t   = 2 t sin ⁡ t + 2 cos ⁡ t

Temos:

∫ - t 2 s e n   t   d t   = t 2 cos ⁡ t - 2 t sin ⁡ t + 2 cos ⁡ t

∫ - t 2 s e n   t   d t   = t 2 cos ⁡ t - 2 t sin ⁡ t - 2 cos ⁡ t

Voltando para a variável x :

∫ 1 x 4 sen ⁡ 1 x d x =   1 x 2 cos ⁡ 1 x - 2 1 x sin ⁡ 1 x - 2 cos ⁡ 1 x

∫ 1 x 4 sen ⁡ 1 x d x =   cos ⁡ 1 x x 2 - 2 sin ⁡ 1 x x - 2 cos ⁡ 1 x

Passo 6

Ok. Agora aplicamos o TFC-Parte 2:

∫ 1 b 1 x 4 sen ⁡ 1 x d x = cos ⁡ 1 b b 2 - 2 sin ⁡ 1 b b - 2 cos ⁡ 1 b - cos ⁡ 1 1 1 2 - 2 sin ⁡ 1 1 1 - 2 cos ⁡ 1 1

∫ 1 b 1 x 4 sen ⁡ 1 x d x = cos ⁡ 1 b b 2 - 2 sin ⁡ 1 b b - 2 cos ⁡ 1 b - cos ⁡ 1 - 2 sin ⁡ 1 - 2 cos ⁡ 1

∫ 1 b 1 x 4 sen ⁡ 1 x d x = cos ⁡ 1 b b 2 - 2 sin ⁡ 1 b b - 2 cos ⁡ 1 b - - cos ⁡ 1 - 2 sin ⁡ 1

∫ 1 b 1 x 4 sen ⁡ 1 x d x = cos ⁡ 1 b b 2 - 2 sin ⁡ 1 b b - 2 cos ⁡ 1 b + cos ⁡ 1 + 2 sin ⁡ 1

Passo 7

E calculamos o limite:

l i m b → ∞ ∫ 1 b 1 x 4 sen ⁡ 1 x d x = l i m b → ∞ cos ⁡ 1 b b 2 - 2 sin ⁡ 1 b b - 2 cos ⁡ 1 b + cos ⁡ 1 + 2 sin ⁡ 1

= l i m b → ∞ cos ⁡ 1 b b 2 - 2   l i m b → ∞ sin ⁡ 1 b b - 2 lim b → ∞ cos ⁡ 1 b + cos ⁡ 1 + 2 sin ⁡ 1

Temos que

l i m b → ∞ cos ⁡ 1 b b 2 = 0

l i m b → ∞ sin ⁡ 1 b b = 0

lim b → ∞ cos ⁡ 1 b = cos ⁡ 0 = 1

Logo:

l i m b → ∞ ∫ 1 b 1 x 4 sen ⁡ 1 x d x = - 2 + cos ⁡ 1 + 2 sen ⁡ 1

Resposta

A integral imprópria é convergente:

∫ 1 ∞ 1 x 4 sen ⁡ 1 x d x = - 2 + cos ⁡ 1 + 2 sen ⁡ 1

Exercício Resolvido #3

CEFET - Cálculo 1 - P3 Romulo 2014.2 – 2b

Calcule as integrais abaixo utilizando integração por substituição simples.

b ) ∫ 0 ∞ 1 + e a t 3 / 2 e - a t d t ,   a > 0

Passo 1

A questão é bizarra, já se prepara...

Eu não vejo de cara nenhuma mudança muito óbvia para fazer. Vou então chamar o termo que está elevado a um expoente mais diferente, então, de outra coisa ( u ) . Além disso, vou forçar o que sobraria (estou falando daquele e - a t ) a virar meu d u :

u = 1 + e a t   ;   d u = a e a t d t → e - a t d t = d u a   e 2 a t

e - a t d t = d u a u - 1 2

Mudamos os limites também, certo?

u 0 = 1 + e a ( 0 ) = 2   ; u ( ∞ ) = 1 + e a ( ∞ ) = ∞

Vamos substituir agora e ver se melhora:

∫ 0 ∞ 1 + e a t 3 / 2 e - a t d t = ∫ 2 ∞ u 3 / 2 d u a u - 1 2

= 1 a ∫ 2 ∞ u 3 / 2 d u u - 1 2 =

Passo 2

Bom, está ruim de trabalhar assim, com o u elevado a 3 / 2 . Vou fazer uma outra mudança para chamar o que seria a raiz de u de w . Lembrando, tenho que fazer o d u e os limites também:

u 1 2 = w   ; d w = 1 2 1 u 1 2 d u → d u = 2 u 1 2   d w

d u = 2 w   d w

w 2 = u 1 2 = 2 1 2 = 2   ; w ∞ = u 1 2 = ∞ 1 2 = ∞

1 a ∫ 2 ∞ u 3 2 d u u - 1 2 = 1 a ∫ 2 ∞ w 3 2 w   d w w 2 - 1 2 = 2 a ∫ 2 ∞ w 4 w 2 - 1 2 d w

A partir daqui temos apenas polinômios.

Passo 3

Me parece que o mais simples é sair por frações parciais! O detalhe é que só temos que dividir o polinômio de cima pelo de baixo, para deixar o grau de cima abaixo do de baixo (os dois estão no grau 4 agora). Para isso, vamos ser malandros e lembrar que

w 4 = w 4 - 2 w 2 - 1 + 2 w 2 - 1 . Portanto:

2 a ∫ 2 ∞ w 4 w 4 - 2 w 2 + 1 d w = 2 a ∫ 2 ∞ w 4 - 2 w 2 + 1 + 2 w 2 - 1 w 4 - 2 w 2 + 1 d w

= 2 a ∫ 2 ∞ 1 + 2 w 2 - 1 w 2 - 1 2 d w

Agora podemos fazer frações parciais naquela divisão de polinômios:

2 w 2 - 1 w 2 - 1 2 = A w + B w 2 - 1 + C w + D w 2 - 1 2 = A w + B w 2 - 1 + C w + D w 2 - 1 2

2 w 2 - 1 w 2 - 1 2 = A w 3 + B w 2 - A w - B + C w + D w 2 - 1 2

A = 0 B = 2 - A + C = 0 - B + D = - 1

A = 0   ; B = 2   ; C = 0   ; D = 1

2 a ∫ 2 ∞ 1 + 2 w 2 - 1 w 2 - 1 2 d w = 2 a ∫ 2 ∞ 1 + 2 w 2 - 1 + 1 w 2 - 1 2 d w

= 2 a w - 2 arctg h ⁡ w 2 ∞ + 2 a ∫ 2 ∞ 1 w 2 - 1 2 d w

Como você deve ter visto, essa última integral não é uma integral direta. Eu preciso de mais um algebrismo para resolvê-la. Faremos uma substituição hiperbólica! Esse caso é o da tangente hiperbólica:

w = tg h ⁡ ( θ ) → d w = sec h 2 ⁡ ( θ ) d θ

∫ 1 w 2 - 1 2 d w = ∫ 1 tg h ⁡ θ 2 - 1 2 sec h 2 ⁡ θ d θ

= ∫ 1 - sec h 2 ⁡ ( θ ) 2 sec h 2 ⁡ θ d θ = ∫ 1 sec h 2 ⁡ θ d θ = ∫ cos h 2 ⁡ θ d θ

= ∫ 1 + cos h ⁡ 2 θ 2 d θ = θ 2 + 1 4 sen h ⁡ ( 2 θ )

Retomando a relação inversa de θ em função de w :

θ 2 + 1 4 senh ⁡ ( 2 θ ) = arctgh ⁡ w 2 + 1 2 ∙ tgh ⁡ w 1 - tg h 2 ⁡ w

Posso, finalmente, juntar tudo que eu integrei!

2 a w - 2 arctg ⁡ w + arctgh ⁡ w 2 + 1 2 ∙ tgh ⁡ w 1 - tgh 2 ⁡ w ∞ 2

2 a w - 1 2 arctg ⁡ w + 1 2 ∙ tgh ⁡ w 1 - tgh 2 ⁡ w ∞ 2

Vamos analisar essa integral imprópria aí com uma outra variável no limite superior:

2 a lim t → ∞ ⁡ t - 1 2 arctg ⁡ t + 1 2 ∙ tgh ⁡ t 1 - tgh 2 ⁡ t - 2 a 2 - 1 2 arctg ⁡ 2 + 1 2 ∙ tgh ⁡ 2 1 - tgh 2 ⁡ 2

Quanto ao termo do limite, repare que o último pedaço vai a para o ∞ , pois o denominador 1 - tgh 2 ⁡ t vai para 0 . O arco tangente vai tender para uma constante. Agora, o primeiro termo, o t , vai para o ∞ . Bom, sabendo que nessa conta toda só teremos constantes e termos que tendem a infinito, a nossa integral divergirá. Ou seja, ela vai para + ∞ !!

∫ 0 ∞ 1 + e a t 3 / 2 e - a t d t = ∞

Questão do mal, coisa horrível...

Resposta

∫ 0 ∞ 1 + e a t 3 / 2 e - a t d t = ∞

Exercício Resolvido #4

UERJ - Cálculo 2 - Lista de Integrais Professora Renata – 37

Calcule a integral imprópria:

∫ - ∞ + ∞ x e - x 2 d x

Passo 1

Aqui temos o caso com limites de integração infinitos. Bom, para resolver isso é necessário calcular a primitiva e analisar os infinitos como limites de variáveis novas. Aqui eu vou calcular por substituição simples essa primitiva:

u = - x 2 → d u = - 2 x d x

∫ x e - x 2 d x = ∫ - e u 2 d u = - e u 2 = - e - x 2 2

Passo 2

Tendo isso, vamos agora para o teorema fundamental do Cálculo. Vamos fazer

∫ - ∞ ∞ f x d x = ∫ - ∞ c f x d x +   ∫ c ∞ f x d x

∫ - ∞ ∞ x e - x 2 d x = ∫ - ∞ c x e - x 2 d x +   ∫ c ∞ x e - x 2 d x

Passo 3

Vamos calcular cada integral separadamente. Para a primeira integral

∫ - ∞ c x e - x 2 d x = lim b → - ∞ ⁡ ∫ b c x e - x 2 d x

∫ b c x e - x 2 d x = - e - c 2 2 + e - b 2 2

Agora vamos calcular o limite

l i m b → - ∞ - e - c 2 2 + e - b 2 2 = - e - c 2 2

Passo 4

Agora vamos calcular a segunda integral.

∫ c ∞ x e - x 2 d x = lim b → ∞ ⁡ ∫ c b x e - x 2 d x

∫ c b x e - x 2 d x = - e - b 2 2 + e - c 2 2

Agora vamos calcular o limite

l i m b → ∞ - e - b 2 2 + e - c 2 2 = e - c 2 2

Passo 5

Agora precisamos juntar os dois resultados!

∫ - ∞ + ∞ x e - x 2 d x = - e - c 2 2 + e - c 2 2 = 0

Resposta

∫ - ∞ + ∞ x e - x 2 d x = 0

Exercício Resolvido #5

UERJ - Cálculo 2 - Lista de Integrais Professora Renata- 35

Verifique se a integral imprópria converge ou diverge:

∫ - ∞ + ∞ e - x d x

Passo 1

Primeiro, a definição do módulo:

f x = - x ,     x < 0 x ,     x ≥ 0

Bom, portanto é como se tivéssemos:

∫ - ∞ + ∞ e - x d x = ∫ - ∞ 0 e x d x + ∫ 0 + ∞ e - x d x

Ou seja, basta integrar as duas e descubro se convergem ou divergem. Há um detalhe, elas são simétricas em relação à origem. Basta calcular uma das duas e multiplicar por 2 :

∫ - ∞ 0 e x d x + ∫ 0 + ∞ e - x d x = 2 ∫ 0 + ∞ e - x d x

= 2 lim a → ∞ ⁡ - e - a + 2 e 0 = 0 + 2 = 2

Converge!

Resposta

A integral converge.

Exercício Resolvido #6

UFRJ - Cálculo 1 - P2 2012.2 – 4

Considere a região infinita R limitada pela curva

y = e - x 2 x 2 + 1 2     - ∞ < x < ∞

e pelo eixo x . Escreva uma integral que represente a área de R e determine, sem calcular a integral, se essa região tem a área finita ou infinita. Justifique sua resposta.

Passo 1

Ora, o enunciado nos fala de uma região limitada pela curva y e pelo eixo x . Essa região é a área entre a curva y e o eixo x , ou seja, a integral de y .

Como os limites de integração são infinitos, trata-se de uma integral imprópria!

O problema quer saber se essa região tem área finita ou infinita. Ou seja, quer saber se o resultado da integral imprópria é um número ou é infinito, ou melhor, se a integral é convergente ou divergente.

Repare, também, que o enunciado nos diz para não calcular a integral. Como vamos saber se a integral é convergente ou divergente sem calculá-la? Vamos usar o Teorema de Comparação!

Queremos saber se a seguinte integral imprópria é convergente ou divergente:

∫ - ∞ ∞ e - x 2 x 2 + 1 2 d x

Temos que usar o Teorema de Comparação que diz que se f ( x ) ≥ g ( x ) , então:

1. Se ∫ - ∞ ∞ f ( x ) d x é convergente, então ∫ a ∞ g ( x ) d x será convergente também.

2. Se ∫ - ∞ ∞ g ( x ) d x é divergente, então ∫ a ∞ f ( x ) d x será divergente também.

Logo, o problema consiste em acharmos uma g ( x ) para que possamos comparar com a função dada e decobrir a convergência ou divergência dela.

Passo 2

f x = e - x 2 x 2 + 1 2

Repare que f - x = f ( x ) . Logo, essa função é par e:

∫ - ∞ ∞ e - x 2 x 2 + 1 2 d x = 2 ∫ 0 ∞ e - x 2 x 2 + 1 2 d x

Vamos dividir a integral em duas:

∫ 0 ∞ e - x 2 x 2 + 1 2 d x = ∫ 0 1 e - x 2 x 2 + 1 2 d x + ∫ 1 ∞ e - x 2 x 2 + 1 2 d x

Passo 3

A primeira integral converge e dá um número (é uma integral definida). Vamos analisar se a segunda converge. Temos que:

e - x 2 x 2 + 1 2 = 1 e x 2 x 2 + 1 2

Para x ≥ 1 :

1 e x 2 x 2 + 1 2 < 1 x 2 + 1 2 < 1 x 2 2 = 1 x 4

Como

∫ 1 ∞ d x x 4 = - 1 3 . 1 x 3 1 ∞ = 0 + 1 3 = 1 3

Se a integral de 1 / x 4 converge, então, 1 e x 2 x 2 + 1 2 converge e, consequentemente:

∫ - ∞ ∞ e - x 2 x 2 + 1 2 d x   t e m   á r e a   f i n i t a

OBS:

Em problemas de convergência em que não podemos calcular a integral (seja porque o enunciado pede ou porque é difícil de calcular), temos que usar o Teorema de Comparação.

Como fizemos aqui:

1 e x 2 x 2 + 1 2 < 1 x 2 + 1 2 < 1 x 2 2 = 1 x 4

O melhor jeito de comparar é especificar um intervalo (ex: x > 1 ), onde a função se comporta de maneira previsível e ir comparando aos poucos até chegar em uma função muito simples.

Resposta

∫ - ∞ ∞ e - x 2 x 2 + 1 2 d x   t e m   á r e a   f i n i t a

Exercícios de Livros Relacionados

Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu