Integrais Impróprias – Funções com Descontinuidade
Produzido por Arthur Melo de AlmeidaTeoria
Integrandos Descontínuos
Agora vamos ver mais um tipo de integral imprópria, que acontece quando a função que estamos integrando é descontínua.
Se é contínua em e possui uma descontinuidade infinita em :
Se é contínua em e possui uma descontinuidade infinita em :
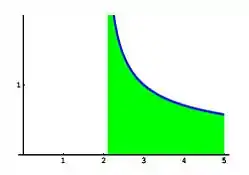
Se tem uma descontinuidade infinita em no meio do intervalo e as integrais e forem convergentes, ou seja, derem como resultado um número, então:
Os problemas de integrais impróprias com integrandos descontínuos podem parecer problemas de integrais definidas a princípio. Por isso, o primeiro passo é identificar se tem uma descontinuidade infinita no intervalo .
Aí eu resolvo a integral, uso o Teorema Fundamental do Cálculo e calculo o limite. Olha só um exemplo camarada aqui:
O denominador se anula em , então esse é um ponto de descontinuidade. E temos:
Observação: Por causa do expoente 2, o denominador sempre tende a zero por valores positivos. Consegue perceber?
Essa descontinuidade infinita ocorre entre os limites de integração dados, e .
Então vamos dividir o intervalo de integração em dois, assim ó:
Mas se eu colocar ali direto vai dar ruim, por causa da descontinuidade. O que eu quero é o limite quando é muito próximo de , pela direita e pela esquerda. Deu pra acompanhar? Vamos fazer
A integral indefinida é
Utilizando o Teorema Fundamental do Cálculo e aplicando os limites:
A outra integral vai ser bem parecida:
Juntando as duas:
Como os dois limites existem, essa integral imprópria é convergente e podemos escrever:
Deu pra pegar a ideia? Então agora é mão na massa!
Exercícios Resolvidos
Exercício Resolvido #1
PUC-RJ - Cálculo B - P3 2013.1 - 1ª
Calcule a integral:
Passo 1
Nesse tipo de questão, temos que estar muito atentos, porque às vezes passa despercebido que aquela função ali dentro da integral tem uma descontinuidade infinita em .
Portanto, esse é um daqueles casos de integral imprópria porque o integrando tem uma descontinuidade infinita no intervalo de integração dado. Repara que, nesse caso, a descontinuidade está em , que é a extremidade do intervalo .
Passo 2
No caso em que a descontinuidade está no limite inferior de integração, substituímos esse limite por e calculamos o limite quando tende a esse valor pela direita:
Para resolver, achamos a integral indefinida e depois substituímos os limites de integração pelo Teorema Fundamental do Cálculo:
Nesse caso, essa integral sai poruma substituição simples:
Substituindo na expressão, vamos ter:
Voltando para :
Passo 3
Utilizando o Teorema Fundamental do Cálculo:
Voltando ao limite da integral imprópria:
Como o limite existe, a integral é convergente.
Resposta
Exercício Resolvido #2
James Stewart, Cálculo Vol. 1, tradução da 5ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2005, pp. 533 ex 37
Diga se a integral converge ou diverge
Passo 1
Novamente, temos que ficar atentos: não pode passar batido o fato de que aquele denominador ali não pode ser igual a . Se calcularmos o limite daquela função quando :
Portanto, esse é um daqueles casos de integral imprópria porque o integrando tem uma descontinuidade infinita no intervalo de integração dado. Repara que, nesse caso, a descontinuidade está em , que faz parte do intervalo de integração .
Passo 2
Como a descontinuidade infinita está no meio do intervalo de integração, esse é aquele caso em que tenho que dividir o intervalo de integração em dois, um que vai do limite inferior até o ponto de descontinuidade e outro que vai desse ponto de descontinuidade até o limite superior:
Aí lembra que eu não vou substituir direto . N verdade, quero o limite quando tende a zero pela direita e pela esquerda, beleza? Por isso que eu vou escrever isso aqui:
Passo 3
Tá tranquilo e favorável até aí?
Então agora vamos achar a primitiva e depois substituir os limites, pode ser?
Nesse caso, essa integral sai por substituição simples:
Substituindo na expressão, vamos ter:
Voltando para :
Passo 4
Utilizando o Teorema Fundamental do Cálculo:
Calculando os limites:
Gente, só existe logaritmo de número positivo, certo? Ou seja, se eu me aproximasse do pelo lado esquerdo daria ruim. Nem existe como isso ser feito. Por aí, já dá para ver que a integral vai divergir. Mas se quisermos calcular o outro limite:
Essa integral diverge, isto é, seu limite não é um número finito.
Resposta
A integral diverge.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
UFRJ - Cálculo 1 - P2 2012.2 - 1b
Calcule as integrais abaixo.
Passo 1
O enunciado nos pede para calcular uma integral definida. Nesse tipo de questão, tem que ter muita atenção, porque é fácil não perceber que aquela questão tem uma descontinuidade.Dá vontade de resolver direto.
Mas quando a função tem uma descontinuidade infinita no intervalo de integração dado, já sabemos que não podemos fazer isso, porque em algum momento estaríamos substituindo um valor naquela função em que ela não é contínua. Saca?
Fique muito atento. Porque essas integrais, de fato, se camuflam facilmente e passam como integrais definidas. Não se deixe enganar, porque se você resolver como integral definida, vai estar conceitualmente errado! Pode ser que, se os planetas se alinharem, o resultado até dê igual, mas o professor provavelmente ainda vai te dar errado, porque você partiu de um conceito errado!
Repara bem: temos uma função . Quando , tende para e tende para
Ou seja, não se trata de uma integral definida simples, e sim, uma integral imprópria! O integrando tem uma descontinuidade infinita no intervalo de integração dado. Repara que, nesse caso, a descontinuidade está em , que é a extremidade do intervalo .
- ''Passo 2
No caso em que a descontinuidade está no limite inferior de integração, substituímos esse limite por r e calculamos o limite quando r tende a esse valor pela esquerda:
Para resolver, achamos a integral indefinida e depois substituímos os limites de integração pelo Teorema Fundamental do Cálculo:
Como se trata da integral de uma função logarítmica vezes uma função polinomial . Vamos tentar o método de integração por partes para achar a primitiva?
Vamos calcular a nova integral por partes de novo:
Aplicando:
Passo 3
Utilizando o Teorema Fundamental do Cálculo:
Voltando ao limite da integral imprópria:
Vamos calcular os limites separadamente:
Observe que nos dois primeiros limites que aparecem, eu teria uma indeterminação do tipo 0. (:
Então o que fazemos? Temos que lembrar daqueles artificiozinhos que aprendemos lá em limites. Manipulamos a expressão de forma a chegar em uma indeterminação do tipo ou e poder utilizar L’Hospital para poder aplicar o limite. Assim:
Tendo indeterminações desse tipo, nós podemos, então, aplicar o nosso amadíssmo L’Hospital (é, parece que você nunca se livra dele mesmo...)
Aplicando L’Hospital:
Aplicando L’Hospital:
Finalmente:
Como o limite existe, a integral converge e podemos escrever:
Resposta
Exercício Resolvido #4
UNICAMP - Cálculo 1 - P3 2008.1 b - 4 b
Determine se as integrais abaixo são divergentes ou convergentes e calcule o valor daquelas que forem convergentes:
Passo 1
Bom, aparentemente, temos uma integral definida para calcular. Você tem que ficar atento e ver se a função não tem uma descontinuidade infinita, porque, se tiver, então ela é imprópria e não pode ser calculada diretamente como uma integral definida.
Nesse problema mais especificamente, o enunciado já te dá a dica, porque ele não pede para você calcular a integral. Ele pede para você dizer se ela é convergente ou divergente. Então fica meio que na cara que essa integral aí é imprópria.
Observa que o não pode ser , senão e vai dar ruim. Claro que também não poderia ser . Mas se você observar, o intervalo de integração vai de a , ou seja, não está dentro desse intervalo. Isso significa que você não precisa se preocupar com ele. Lembre-se que você tem que se preocupar com descontinuidades em pontos dentro do intervalo de integração, beleza?
Vamos calcular o limite da função quando para garantir que a descontinuidade que ela tem nesse ponto é infinita?
Ok. Tenho uma descontinuidade infinita em . Então trata-se de um caso de integral imprópria com integrando descontínuo.
Nesse caso, a descontinuidade está em , que é a extremidade do intervalo .
- ''Passo 2
No caso em que a descontinuidade está no limite inferior de integração, substituímos esse limite por e calculamos o limite quando tende a esse valor pela direita:
Para resolver, achamos a integral indefinida e depois substituímos os limites de integração pelo Teorema Fundamental do Cálculo:
Para calcular essa integral indefinida, basta você lembrar que trata-se daqueles casos classiquinhos de substituição simples, em que eu tenho um ali e um , que é derivada dele. Então aquele ali está pedindo para ser chamado de , não é?
Substituindo na expressão, vamos ter:
Voltando para :
- ''Passo 3
Utilizando o Teorema Fundamental do Cálculo:
Voltando ao limite da integral imprópria:
Logo, o limite existe e a integral é convergente!
Resposta
Exercício Resolvido #5
Determine se a integral abaixo é divergente ou convergente e calcule o valor caso seja convergente:
Passo 1
Bom, aparentemente, temos uma integral definida para calcular. Você tem que ficar atento e ver se a função não tem uma descontinuidade infinita, porque, se tiver, então ela é imprópria e não pode ser calculada diretamente como uma integral definida.
Nesse problema mais especificamente, o enunciado já te dá a dica, porque ele não pede para você calcular a integral. Ele pede para você dizer se ela é convergente ou divergente. Então fica meio que na cara que essa integral aí é imprópria.
Se reescrevermos a integral da forma:
Dá pra sacar que o não pode ser , senão ficamos com e vai dar ruim. Claro que também não poderia ser . Mas se você observar, o intervalo de integração vai de a , ou seja, não está dentro desse intervalo. Isso significa que você não precisa se preocupar com ele. Lembre-se que você tem que se preocupar com descontinuidades em pontos dentro do intervalo de integração, beleza?
Vamos calcular o limite da função quando para garantir que a descontinuidade que ela tem nesse ponto é infinita?
Fazendo L’Hospital, ficamos com:
Ok. Tenho uma descontinuidade infinita em . Então trata-se de um caso de integral imprópria com integrando descontínuo.
Nesse caso, a descontinuidade está em , que está dentro do intervalo . Sendo assim é conveniente a gente escrever a integral dessa forma:
Passo 2
Bem, como não podemos integrar diretamente, porque em da problema, substituímos esse limite de integração por e calculamos o limite quando tende a esse valor pela direita e pela esquerda.
O limite pela esquerda é o da primeira integral porque o intervalo está a esquerda de e a segunda integral leva o limite pela direita porque o intervalo está a esquerda de , beleza?
Para resolver, achamos a integral indefinida e depois substituímos os limites de integração. Essa integral parece um pouco complicada, mas fazendo integração por partes, tiramos de letra, quer ver?
Se
Então:
A segunda integral a gente tira por frações parciais, saca só:
Então ficamos com o seguinte sistema de equações:
O que nos leva à:
E então:
E a integral imprópria fica:
Passo 3
Aplicando os limites, vamos ter, pra primeira integral:
No limite inferior, vamos acabar tendo sempre um multiplicado por alguma coisa. Como esse logaritmo é igual à , nos sobra:
E se olharmos bem, esse limite vai pro infinito! Veja só, o limite acima e o abaixo são a mesma coisa:
O único limite ai que tem um resultado é o último. Vamos ter que esse limite vai ser:
Só isso já é o suficiente galera! Se essa integral diverge, não tem como
Que faltou calcular, convergir. Mas, calculando mesmo assim só pra n deixar sem fazer: