Propriedades De Integrais
Produzido por Arthur Melo de AlmeidaTeoria
Existem algumas propriedades de integrais que são bastante importantes no cálculo e é essencial que elas estejam no sangue, porque você vai ter que usá-las o tempo todo!
Mas não se preocupe, são relações bem simples e, logo, logo, você estará usando sem nem sentir!
O Responde Aí preparou um vídeo super completo com todas as propriedades de integrais pra você arrasar na prova! Dá uma conferida 👇👇👇
📢 Clique para saber mais:
Propriedade 1 - Soma e Subtração de Integrais
Essa propriedade diz que a integral da soma ou subtração de funções é a soma ou subtração das integrais:
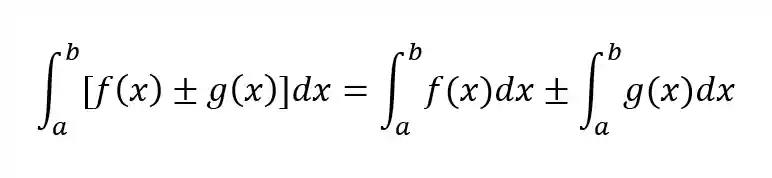
Por exemplo:
Propriedade 2 - Integral Múltipla de uma Constante
A integral de uma função vezes uma constante é igual à integral daquela função multiplicada pela constante.
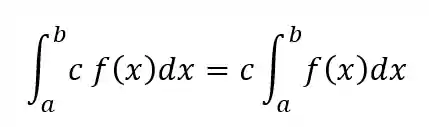
Em outras palavras, a constante pode ser colocada “para fora” da integral!
Por exemplo:
Propriedade 3 - Integral com Intervalo igual a zero
Quando uma integral tem limites superior e inferior iguais seu resultado é nulo!
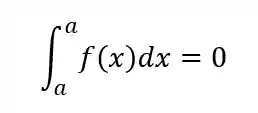
Propriedade 4 - Integral de uma Constante
A integral de uma função constante,
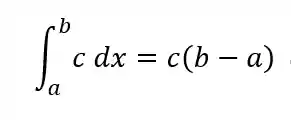
Propriedade 5 - Integral com Limites Invertidos
Ao trocar os limites de integração inferior e superior, troca-se o sinal da integral:
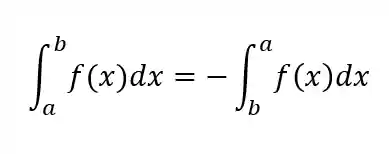
Por exemplo:
Propriedade 6 - Soma de Intervalos
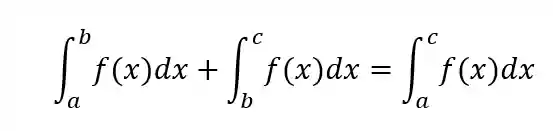
Pra ficar mais claro, considere a seguinte área sobre a curva:
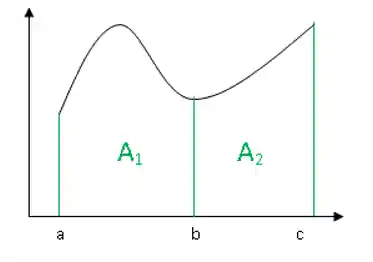
Podemos dizer que:
Então:
Propriedade 7 - Sinal de uma Integral
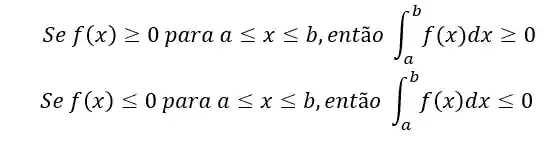
Para lembrar dessa propriedade, facilita lembrar da interpretação como área.
- Se
é sempre maior que zero no intervalo , então a integral será sempre igual à área da região delimitada naquele intervalo. Lembre-se que área é sempre um número positivo!
- Por outro lado, se
é sempre menor que zero naquele intervalo, a integral será sempre igual ao simétrico da área delimitada naquele intervalo. Como a área é sempre um número positivo, então a integral será um número negativo!
Resumo: Propriedades das Integrais
Agora, pra fechar, se liga nesse resumo com todas as propriedades de integrais que você precisa saber! 👇👇👇

Agora, vamos praticar com exercícios?