Limites Laterais
Produzido por Arthur Melo de AlmeidaTeoria
Limites laterais nada mais é do que o valor do qual uma função
Limites Laterais e a Existência do Limite
A definição formal de limites laterais ficou um pouco confusa?!
Não se preocupe! Se liga nesse vídeo que o Responde Aí separou especialmente pra você, com linguagem simples, de aluno pra aluno👇 🧡
Ou continua comigo no textinho! 😁
Pra ficar mais claro o que é limites laterais, eu quero que você considere a seguinte função
Podemos desenhar seu gráfico:
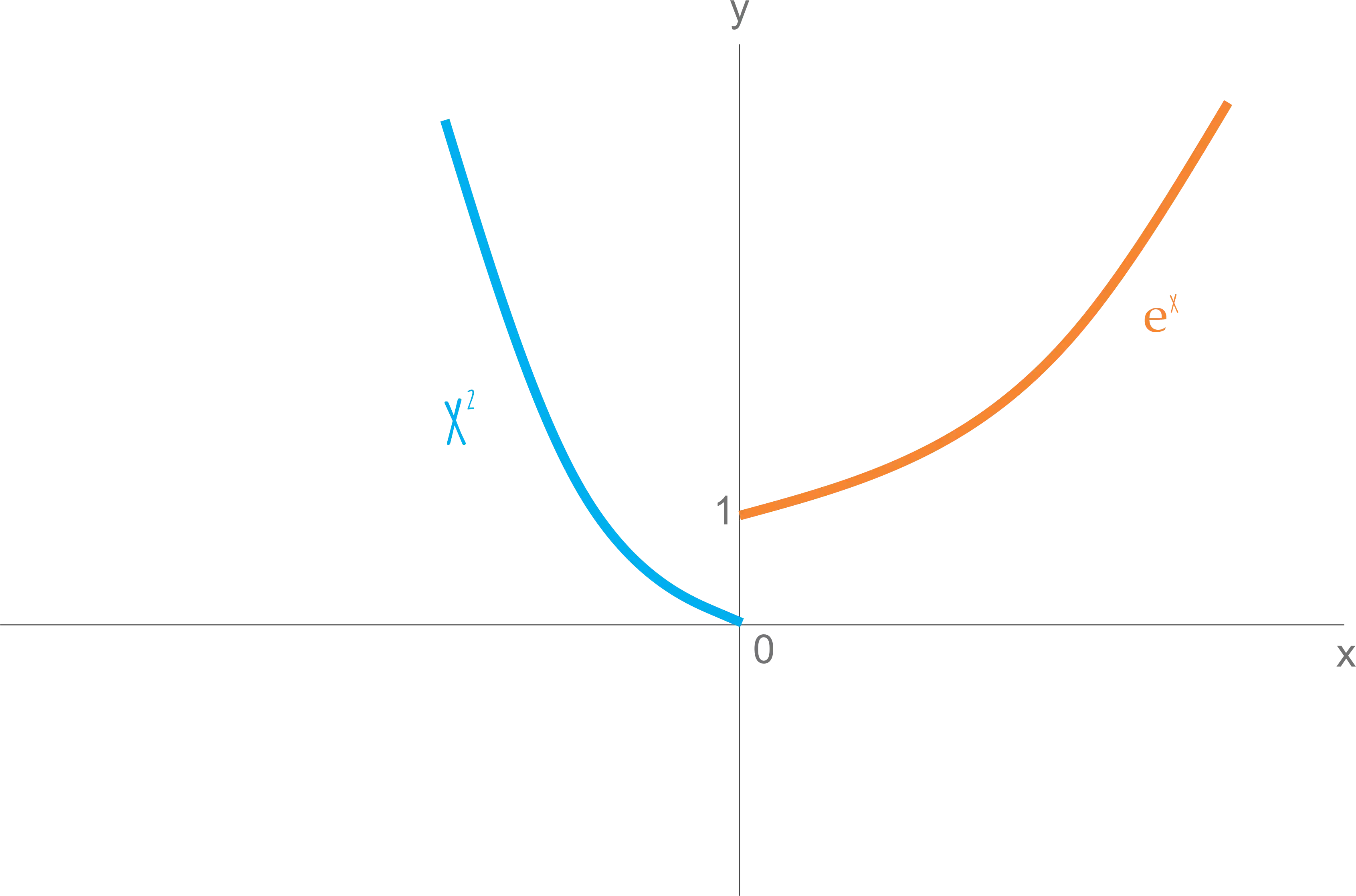
No gráfico acima, veja o que acontece com a função próximo do ponto
Se você tentar aproximar o
Na direita temos a função
Pela esquerda, é o
Isso que você terminou de ver é a notação de limites laterais! De uma forma geral temos:
Se aproximarmos
-Opa, mas no caso geral o limite tanto pela direita quanto pela esquerda tende a
Excelente observação! É ai que esta o pulo do gato! 🐱
Quando os limites laterais não batem, dizemos que, o limite não existe!
Existem duas regras que o limite deve seguir para existir:
- Limites laterais não podem explodir para
; - Limites laterais devem possuir o mesmo valor.
Exemplo: Limites laterais de f(x)=x²
Vimos um exemplo onde os limites laterais não existem! Agora vamos ver um caso onde eles existam!
Considere a função
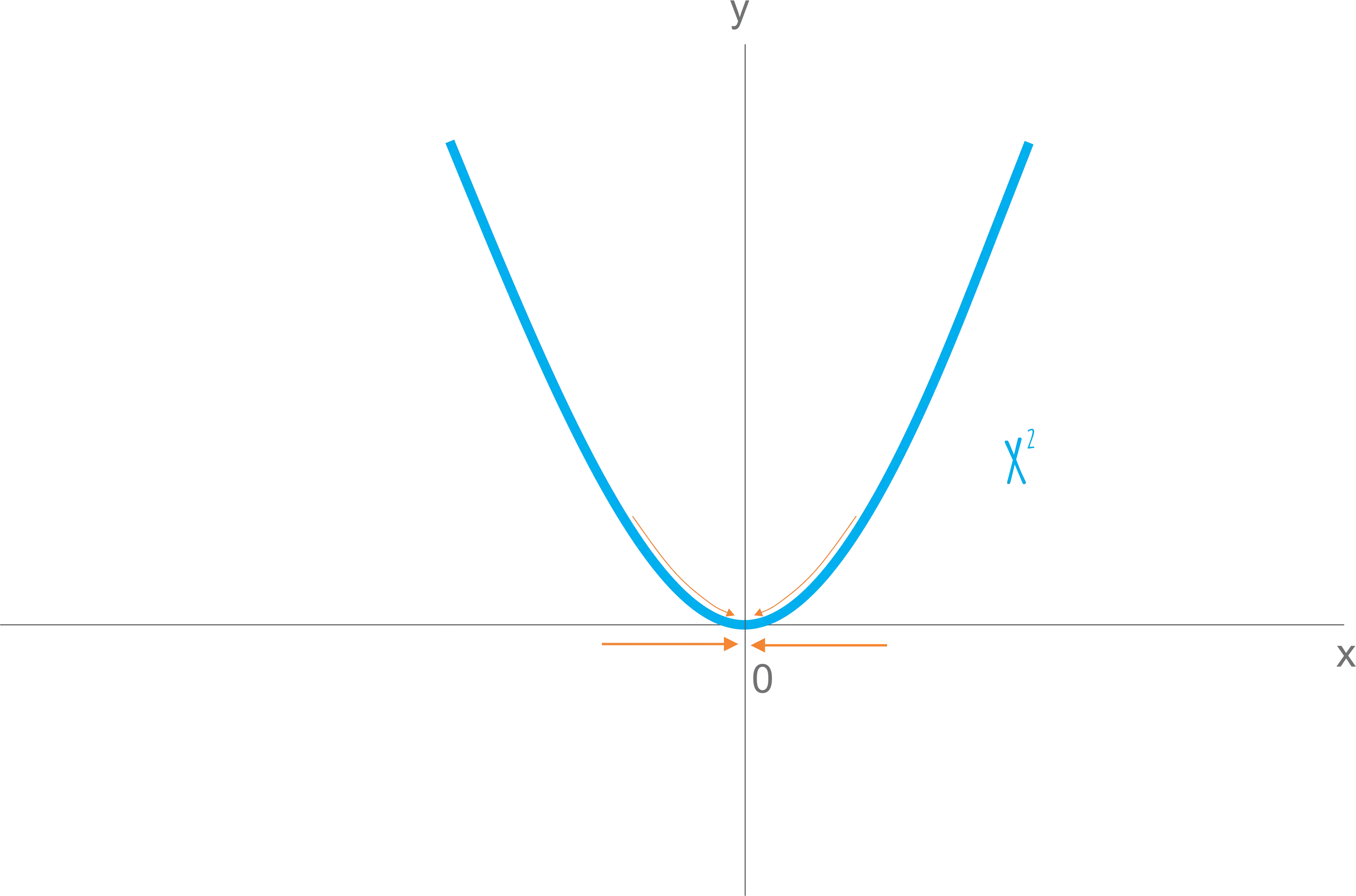
Calculando os limites laterais, temos:
Se você ficar na dúvida, você pode ir substituindo valores menores do que
Agora vamos praticar com exercícios?