Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 26

14.26. Utilize um dispositivo gráfico como no Exemplo 4 (ou Método de Newton ou um determinador de raízes) para estabelecer os pontos críticos de f com arredondamento na terceira casa decimal. Em seguida classifique o ponto crítico e determine o valor mais alto e o mais baixo do gráfico.

f x , y = e x + y 4 - x 3 + 4 cos ⁡ y

Passo 1

Faaala galera! Beleza? Então, nós temos aqui a função

f x , y = e x + y 4 - x 3 + 4 cos ⁡ y

e queremos usar um método gráfico para determinar os pontos críticos de f , ou seja, os pontos ( a , b ) tais que f x a , b = 0 e f y a , b = 0 .

Depois de obter os pontos críticos, vamos classificar se eles são de máximo, mínimo ou de sela. Como fazemos isso?

Para uma variável nós usávamos o teste da derivada segunda. Para duas variáveis, vamos fazer algo parecido, mas da seguinte forma.

Seja D o seguinte determinante

D = f x x a , b f x y a , b f y x a , b f y y a , b

Então:

D = f x x a , b ⋅ f y y a , b - f x y a , b ⋅ f y x a , b

Além disso, pelo teorema de Clairaut: f x y a , b = f y x a , b .

Portanto,

D = f x x a , b ⋅ f y y a , b - [ f x y ( a , b ) ] ²  

Os critérios são:

Se D > 0 e f x x a , b > 0 , então f a , b é um mínimo local.

Se D > 0 e f x x a , b < 0 , então f a , b é um máximo local.

Se D < 0 , então f a , b não tem máximo nem mínimo local e ( a , b ) é dito um ponto de sela.

Agora estamos prontos para responder a questão. Vamos lá!

Passo 2

Beleza, a primeira coisa que a gente tem que fazer é ver o gráfico

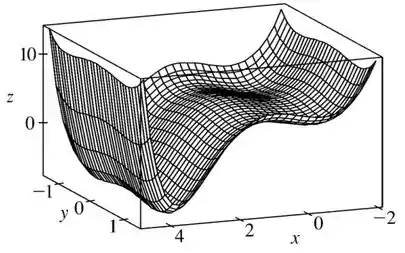
Agora vamos ver mais dois gráficos, os gráficos das derivadas:

Podemos calcular a derivada de f com relação a x :

f x = ∂ ∂ x e x + y 4 - x 3 + 4 cos ⁡ y

f x = e x - 3 x 2

Essa derivada é exibida no gráfico abaixo:

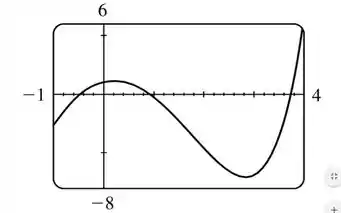
Vamos ver mais ou menos onde f x = 0 , que vai ser quando a curva cruza o eixo das coordenadas. Vai ser mais ou menos

x ≈ - 0,459 ; 0,910 ; 3,733

E agora o gráfico de f y , calculando a derivada de f com relação a y :

f y = ∂ ∂ y e x + y 4 - x 3 + 4 cos ⁡ y

f y = 4 y 3 - 4 sin ⁡ y

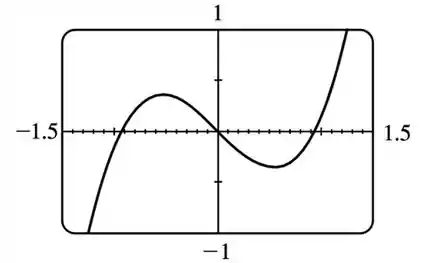
Vamos usar o mesmo esquema

y ≈ - 0,929 ; 0 ; 0,929

Esses são os pontos críticos então.

Passo 3

Se a gente usar uma calculadora ou algum outro programa para igualar as derivadas à 0, acharemos os pontos:

- 0 , 459 ;   0 ; 0 , 910 ;   0 ;   0 , 910 ;   0.929 ;   0 , 910 ;   - 0 , 929

3 , 733 ; 0 ; 3 , 733 ;   0.929 ; ( 3 , 733 ; - 9 , 929 )

Passo 4

Já temos nossos pontos de interesse, mas falta dizer se são máximos, mínimos ou pontos de sela. Para isso a gente precisa da segunda derivada, vamos usar

D = f x x a , b ⋅ f y y a , b - [ f x y ( a , b ) ] ²  

Vamos calcular as segundas derivadas então

f x x = ∂ f x ∂ x

f x = e x - 3 x 2

Agora derivamos isso em relação a x

f x x = ∂ e x - 3 x 2 ∂ x = e x - 6 x

A outra derivada que precisamos é

f y y = ∂ f y ∂ y

f y = 4 y 3 - 4 sin ⁡ y

Derivando em relação a y

f y y = ∂ 4 y 3 - 4 sin ⁡ y ∂ y = 12 y 2 - 4 cos ⁡ y

E a última derivada que precisamos é

f x y = ∂ f x ∂ y

ou f x y = ∂ f y ∂ x

f x = e x - 3 x 2

Vamos derivar isso em relação a y

f x y = ∂ e x - 3 x 2 ∂ y = 0

Então

D x , y = e x - 6 x ⋅ 12 y 2 - 4 cos ⁡ y - 0 2

Passo 5

Agora vamos verificar a natureza dos pontos críticos.

Vamos testar para o ponto - 0 , 459 ;   0 :

D - 0 , 459 ;   0 = - 13 , 55 < 0

Então é um ponto de sela.

Agora o ponto ( - 0 , 459 ;   0 , 929 )

D - 0 , 459 ;   0 , 929 = e - 0 , 459 - 6 - 0 , 459 ⋅ 12 0 - 4 cos ⁡ 0

D - 0 , 459 ; 0 , 929 = 29 , 65 > 0

Vamos checar f x x

f x x = e - 0 , 459 - 6 - 0 , 459 = 3 , 38 > 0

Então é um ponto de mínimo.

Agora o ponto ( - 0 , 459 ;   - 0 , 929 )

D - 0 , 459 ; -   0 , 929 = - 45 , 85 < 0

Então é um ponto de sela.

Agora o ponto (0,910; 0)

D 0 , 910 ;   0 = 11,9 > 0

Vamos checar f x x

f x x = e 0 , 910 - 6 0 , 910 = 5 , 46 > 0

Então é um ponto de mínimo.

Agora o ponto ( 0 , 910 ;   0 , 929 )

D 0 , 910 ;   0 , 929 = - 26 , 05 < 0

Então é um ponto de sela.

Agora o ponto (0.910, -0.929)

D 0 , 910 ; - 0 , 929 = 40 , 30 > 0

Vamos checar f x x

f x x = e 0 , 910 - 6 0 , 910 = 5 , 46 > 0

Então é um ponto de mínimo.

Agora o ponto ( 3 , 73 3 ;   0 )

D 3 , 733 ;   0 = - 77 , 62 < 0

Então é um ponto de sela.

Agora o ponto (3,733; 0,929)

D 3 , 733 ;   0 , 929 = 169,87 > 0

Vamos checar f x x

f x x = e 3 , 733 - 6 3 , 733 = 19 , 4 > 0

Então é um ponto de mínimo.

Agora o ponto ( 3,733 ;   - 0,929 )

D 3 , 733 ;   - 0 , 929 = - 262,81 < 0

Então é um ponto de sela.

Resposta

Os pontos de sela são

- 0 , 459 ;   0 ;   - 0 , 4 59 ;   - 0 , 929 ; 0 , 910 ;   0 , 929 ; 3 , 733 ;   0 ;   3 , 733 ;   - 0 , 929

Os pontos de mínimos são

- 0 , 459 ;   0 , 929 ; 0 , 910 ;   0 ; 0 , 910 ;   - 0 , 929 ; 3 , 733 ;   0 , 929

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estude com relação a máximos e mínimos locais a função f x , y = d) x 2 - y 2 + 4 z 2 + 2 x z - 4 y z - 3 x - 6 z
Considere as reta reversas r e s de equações x , y , z = 0,0 , 2 + λ 1,2 , 0 ; λ ∈ R E x , y , z = 0,0 , 4 + μ 1,1 , 1 ; μ ∈ R Respectivamente. Determine P e Q , com P ∈ r e Q ∈ s de modo que distânci
Seja f ( x , y ) de classeC 2 e seja ( x 0 ,y 0 , z 0 ) ponto no interior D f . Suponha que ( x 0 , y 0 , z 0 ) ponto crítico de f . Prove: ∂ 2 f ∂ x 2 x 0 , y 0 , z 0 ≤ 0 ,∂ 2 f ∂ y 2 x 0 , y 0 , z 0
Estude com relação máximos e mínimos locais da função f x , y = g) x 2 + 2 x y + 4 y 2 - 6 x - 12 y 3
Determine o ponto do plano 3 x + 2 y + z = 12 cuja soma dos quadrados das distâncias a 0,0 , 0 e ( 1,1 , 1 ) seja mínima.