Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.7 - Ex. 36
Se uma função de uma variável é contínua em um intervalo e tem um único ponto crítico, então um máximo local tem de ser um máximo absoluto. Mas isso não é verdadeiro para as funções de duas variáveis. Mostre que a função
Tem exatamente um ponto crítico, onde tem um máximo, local, porém este não é um máximo absoluto. Em seguida utilize um computador com uma escolha conveniente de janela de inspeção e ponto de vista para ver como isso é possível.
Passo 1
Opa, tudo bom? Questãozinha de provar proposição, vamos lá!
O contexto da questão nos diz que: Pra uma função de uma variável com APENAS um ponto crítico, se esse ponto for um máximo local ele obrigatoriamente é um máximo global!
É tranquilo afirmar isso para uma função com uma variável! Mas com duas variáveis a história já é outra, e é isso que a questão pede pra gente provar!
Temos a função
Que possui APENAS um ponto crítico/máximo local.
E precisamos mostrar que existem outros pontos com valores de maiores que o desse máximo local.
Para isso a gente vai primeiro identificar esse ponto crítico/máximo local! E pra isso a gente precisa procurar um ponto onde e sejam iguais a !
Em seguida, pra confirmar que esse é um máximo local, a gente vai jogar o ponto na seguinte fórmula
Onde se
então é um mínimo local.
então é um máximo local.
então não é nem mínimo e nem máximo local.
Ora, mas se o nosso ponto for um máximo local e encontrarmos um outro ponto onde a função tem um valor maior que esse máximo então nós provamos que este não era um máximo absoluto!
Passo 2
Primeiro precisamos encontrar o ponto de interesse! Estamos buscando um ponto onde
Mas para isso precisamos encontrar essas derivadas!
Para a função
Encontramos da seguinte forma
Da mesma forma obtemos
Passo 3
Igualando essas expressões a
Para
Substituindo o valor de na expressão de
Veja que essa expressão só é verdadeira para ou , certo? Mas se a gente substituir na expressão de olha o que acontece:
E isso só aconteceria para tendendo ao infinito negativo!
Então daí a gente sabe que o valor de que estamos buscando é !
Substituindo em a gente encontra
Logo nosso ponto é
Passo 4
Já temos nosso ponto de interesse, mas falta dizer se é mesmo um ponto de máximo, para isso a gente precisa da fórmula
Onde se
então é um mínimo local.
então é um máximo local.
então não é nem mínimo e nem máximo local (um ponto de sela).
Mas primeiro precisamos encontrar as segundas derivadas!
Seja
Então
Da mesma forma, para
E por fim
ou
De forma que
Derivando em relação a
Passo 5
Agora vamos verificar a natureza dos pontos críticos.
Vamos testar para o ponto
Analisando
Então é um ponto de máximo local, assim como o enunciado pediu para provarmos!
Substituindo o ponto na função
E nossa fórmula provou que era um ponto de máximo local, certo?
Mas veja que o termo dominante dessa expressão é ! E conforme aumenta negativamente, maior é o valor de !
Se por exemplo substituirmos e nós temos
E isso já é bem maior que o valor do nosso máximo local que encontramos em ! Então de fato, esse não era nosso máximo global.
Passo 6
Vamos verificar o comportamento dessa função usando o gráfico! Para isso a gente pode jogar nossa função na calculadora 3D do GeogGebra (geogebra.org/calculator) e obter o seguinte gráfico:
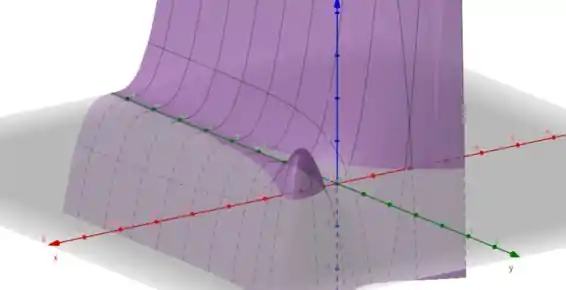
Resposta
O ponto é o máximo local da função mas não é o máximo global.