Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.7 - Ex. 20
20. Existem determinadas reações químicas nas quais as concentrações constituintes oscilam periodicamente com o tempo. O sistema
é um caso particular de um modelo, conhecido como bruxelador, desse tipo de reação. Suponha que b é um parâmetro positivo e considere soluções no primeiro quadrante do plano .
(a) Mostre que o único ponto crítico é .
(b) Encontre os autovalores do sistema linear aproximado no ponto crítico.
(c) Classifique o ponto crítico quanto a tipo e estabilidade. Como a classificação depende de ?
(d) Quando b aumenta e passa por determinado valor crítico , o ponto crítico muda de assintoticamente estável para instável. Qual é esse valor ?
(e) Desenhe trajetórias no plano de fase para valores de ligeiramente menores e ligeiramente maiores do que . Observe o ciclo limite quando ; o bruxelador tem um ponto de bifurcação de Hopf em .
(f) Desenhe trajetórias para diversos valores de e observe como o ciclo limite se deforma quando aumenta.
Passo 1
Logo, o único ponto crítico de fato será... .
Passo 2
Para encontrar os autovalores do sistema linear nesse ponto crítico devemos encontrar o sistema linear que aproxima o não linear...
Agora encontremos a jacobiana disso:
Substituindo o ponto de interesse ...
Então o sistema linear próximo de será:
Passo 3
Beleza! Então agora vamos mandar a ver e buscar os autovalores da nossa matriz de coeficientes:
Calculando então os autovalores dessa matriz...
Simplificando essa equação...
Multiplicando em ambos os lados por apenas para simplificar...
Resolvendo essa equação do segundo grau...
Chamando apenas para simplificar a análise
Aqui, a estabilidade então vai depender totalmente de quem é o nosso (no caso ):
- Se , então...
- Se
- Se
- Se
- :
- :
- :
De modo que mesmo subtraído, vai ser maior que e portanto teremos um sistema instável.
E, portanto, teremos como resposta para valores imaginários conjugados. Nesse caso, como é positivo a parte real será também e, portanto, o sistema será instável mas em espiral.
Nessa condições, continuaremos a ter valores imaginários para , mas dessa vez teremos um sistema assintoticamente estável e em espiral, por causa da parte real ser dessa vez negativo.
Nessas condições, a raiz volta a ser real, mas ela terá um valor abaixo do módulo , isso significa que mesmo somando...
Será negativa, saca? Já que a parte real é um número negativo “maior”: Sistema assintoticamente estável
Lembre-se de que , só vão mudar os intervalos, mas a análise é a mesma!
Passo 4
Repare no passo anterior que o valor de que separa o mundo do estável do instável, acontece no , já que é instável e temos sistemas estáveis.
Como ...
Então...
Passo 5
Usando o mesmo código da questão anterior, só mudando a equação de definição do nosso sistema de EDO para o as nossas equações atuais:
Dessa forma aqui:
E escolhendo alguns pontos iniciais, como o ponto ou , e principalmente já que , perceba que sempre as trajetórias embora sejam instáveis, elas tendem ir para um círculo:
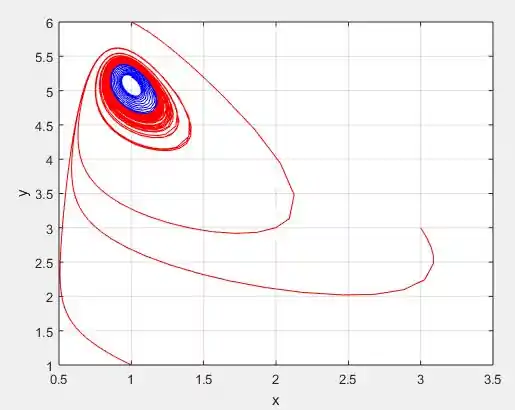
Se escolhermos agora...
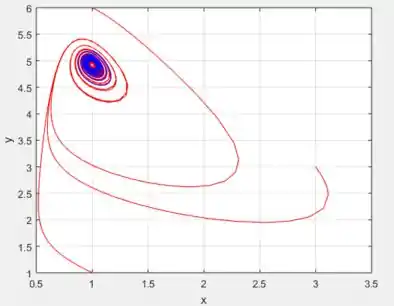
Veja que o sistema se torna estável e todas as curvas tendem para o mesmo ponto:
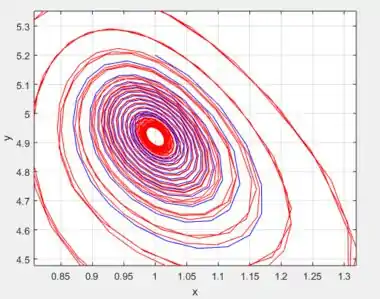
Essa é a mesma figura anterior só que com um zoom pra você ver que de fato, todo mundo estão tendendo ao mesmo ponto provando eu de fato o sistema fica estável!
Passo 6
Se fizermos agora ir aumentando mantendo as mesmas condições iniciais que determinamos...
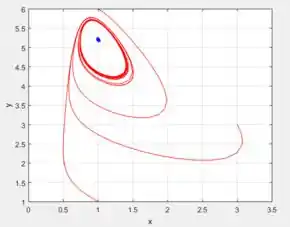
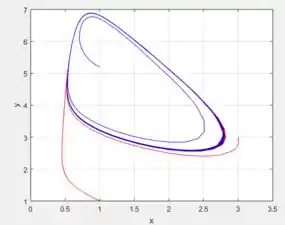
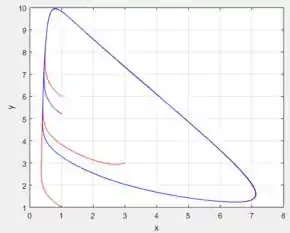
De fato, cada vez mais o círculo que no qual as soluções tendem, vão se deformando ainda mais e rapidamente conforme aumentamos , sacou?
Resposta
Ei, a resposta está no passo a passo :)