27.
Passo 1
Neste exercício, vamos calcular a integral abaixo, usando método da substituição:
Fazendo – se
Teremos:
Para resolver a questão, devemos somar , lembrando que isso não modifica o valor, pois estamos somando 0. (
Portanto,
Divida a integral em duas,
Passo 2
No final do livro, em Tabelas de integrais, temos:
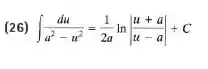
Assim, temos:
Substituindo