Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.7 - Ex. 8

8. x = y^2 + 1 , x = (1)/(2) , y = - 2 e y = 2

Passo 1

Temos que os f ( y ) são:

f_1 (y) = y^2 + 1

f_2 (y) = (1)/(2)

O gráfico dessa equação é o seguinte:

No eixo x temos: (1)/(2) <= x <= 5

No eixo y temos: - 2 <= y <= 2

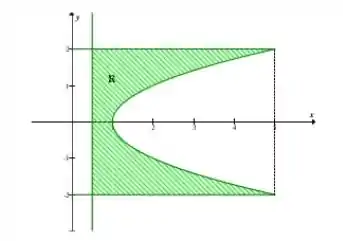
Como podemos observar, temos uma espécie de parábola deitada. Podemos obter a área desse solido, subtraindo f_1 ( y ) que representa a parte maior, pelo f_2 ( y ) .

A (y) = pi (f_1 (y) - f_2 (y))

Passo 2

Para obtermos o volume gerado pela revolução de R em torno do eixo y, usaremos a seguinte formula:

V = pi int_a^b [A (y)]^2 d y

Passo 3

Portanto, o volume é:

V = 2 pi int_0^2 [(y^2 + 1)^2 - ((1)/(2))^2] d y

Observe que nesse caso tivemos um 2 pi ao invés de pi . Isso ocorreu pois nesse caso, temos uma figura simétrica, ou seja, ambos os lados têm o mesmo volume. Assim consideremos duas vezes o mesmo volume, por isso esse 2 na frente. Uma forma alternativa, seria fazer com o intervalo de -2 a +2, mantendo um pi antes da integral.

= 2 pi int_0^2 (y^4 + 2 y^2 + 1 - (1)/(4)) d y

2 pi int_0^2 (y^4 + 2 y^2 + (3)/(4)) d y

2 (pi ((y^5)/(5) + (2)/(3) y^3 + (3)/(4) y)|_0^2 =

= pi ((32)/(5) + (16)/(3) + (3)/(2))

= (397 pi)/(30) u . v .

Resposta

(397 pi)/(30) u . v .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 2 em torno de B C .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 1 em torno de O A .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 2 em torno de AB .
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 2 em torno de O A
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta especificada: R 3 em torno de B C .