Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 35
Seja uma função de duas variáveis que tenha derivadas parciais contínuas e considere os pontos , , e . A derivada direcional em na direção do vetor é , e a derivada direcional em na direção é . Determine a derivada direcional de em na direção do vetor .
Passo 1
Opa, tudo tranquilo? Questãozinha de derivada direcional, vamos lá!
A questão nos diz que existe uma função e descreve as direções e e suas derivadas.
Em seguida ela nos pede para determinar a derivada dessa função na direção . Para visualizar melhor vamos botar isso num plano!
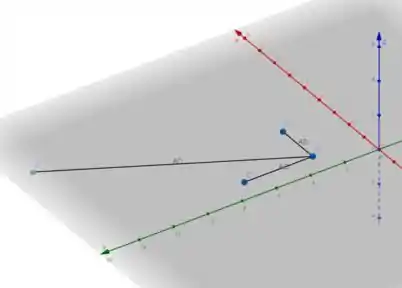
Disso tiramos duas conclusões importantíssimas:
A direção é exatamente já que ela segue paralela ao eixo ;
A direção é exatamente já que ela segue paralela ao eixo ;
Ora, se eu tenho uma derivada na direção de então eu tenho ! Da mesma forma, se eu tenho uma derivada na direção de então eu tenho .
Além disso, a derivada direcional de num ponto em uma direção unitária qualquer é dada por
Onde o gradiente da função é o conjunto das derivadas parciais e (que nós acabamos de descobrir quem eram).
Dessa forma, só precisamos substituir os valores que temos nessa fórmula e partir pro abraço!
Passo 2
Nós vimos que como a direção do vetor é então
Mas o enunciado nos disse que a derivada direcional na direção é . Assim
Da mesma forma, como a direção do vetor é
Mas o enunciado nos disse que a derivada direcional na direção é . Assim
Então nosso gradiente, que é dado por
Fica assim no ponto
Ou com os valores do enunciado
Passo 3
Queremos a derivada direcional de em na direção do vetor
Onde representa um vetor unitário na direção de e pode ser encontrado assim
A direção de é dada da seguinte forma
Agora podemos calcular o módulo
De forma que é
Substituindo na fórmula da derivada direcional
Realizando o produto escalar