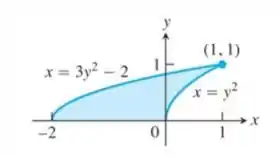
39 – A região apresentada aqui gira em torno do eixo x para gerar um, sólido. Qual método (do disco, do anel, da casca) você usaria para determinar o volume do sólido? Quantas integrais seriam necessárias em cada caso? Explique
Passo 1
Pelo método do disco teremos:
Como esta em torno do eixo x, teremos que organizar a função:
Utilizaremos a fórmula:
Assim teremos:
Inserindo na Integral:
Como não solicita que resolvamos o exercício, podemos concluir que pelo método do disco duas integrais são necessárias! Não seria necessário nem demonstrar o apresentado apenas observar que como requer a integral de V1 e V2 ela necessitará de no mínimo duas integrais.
Passo 2
Pelo método do anel:
Calcular o primeiro volume:
No qual:
E limites de integração seriam:
Calcular o segundo volume:
No qual:
E limites de integração seriam:
Assim seriam necessárias Duas Integrais.
Passo 3
Pelo método da casca:
Observe que deveremos achar a altura, para isto fazemos:
E os limites de integração seriam:
Podemos concluir que seriam necessárias apenas uma integral, sendo este método mais eficiente.
Resposta
O método mais eficiente é o da casca.