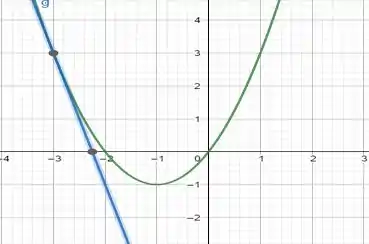
5.(a)Encontre a inclinação da reta tangente à parábola

Usando a Definição 1

Usando a Equação 2

(b) Encontra a equação da reta tangente da parte (a)

(c) Faças os gráficos da parábola e da reta tangente. Como verificação dê um zoom em direção ao ponto até que parábola e a reta tangente fiquem não distinguíveis.

Sem mais enrolação, vamos começar com os cálculos até porque a matéria é Cálculo 1 né!

O ponto de tangência é o ponto , então:

A questão já nos dá o

Pela definição 1:

Fatorando o , pois se substituirmos o valor de na expressão acima, teremos uma indeterminação do tipo .

“Cortando” o no denominador (parte de cima) e no numerador (parte de cima), temos:

Pela definição 1, o coeficiente angular da reta é , faremos agora pela equação e tem que dar o mesmo resultado hein! Serve até como prova real.

Anotando algumas coisas para não nos enrolarmos:

isso foi dado no problema hein, não esquece:

Substituindo tudo no cálculo do limite temos:

Botando o em evidência, temos:

Cortando o de cima e de baixo, temos:

Obaaa! Deu igual, estamos no caminho certo!

Para não ficar muito longo o passo , iremos achar a equação da reta tangente e o gráfico da curva com a reta tangente nesse passo.

Lembrando que a equação da reta é da seguinte forma:

Em que o ponto e

(c) Agora faremos o gráfico da curva e da reta tangente:

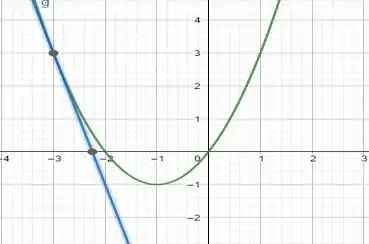
Prontinho!