Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.Revisão - Ex. 89

Ache a área da região limitada pelas curvas x = y^2 e x = y^3 .

Passo 1

Para essa questão faremos a integração em y.

Os pontos de interseção entre as curvas nos fornecem os limites de integração:

y^2 = y^3

P 1 (0,0) ; P 2 ( 1,1 )

Veja o esboço das curvas para uma melhor compreensão:

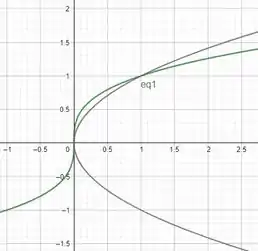
Portanto, como integraremos em y , a função que irá nos fornecer a área será: f (y) = y^2 - y^3 .

Á r e a = int_0^1 (y^2 - y^3) d y

Integrando e substituindo os limites:

Á r e a = ((y^3)/(3) - (y^4)/(4)) (1)/(0) = (1)/(12) u . a .

Resposta

Á r e a = (1)/(12) u . a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A curva com a equação y 2 = x 2 x + 3 é chamada cúbica de Tschirnhausen. Se você colocar essa curva em um gráfico, verá que parte dela forma um laço. Encontre a área dentro desse laço.
Encontre os valores de c tal que a área da região limitada pelas parábolas y = x 2 - c 2 e y = c 2 - x 2 seja 576 .
Para quais valores de m a reta y = m x e a curva y = x x 2 + 1 delimitam uma região? Encontre a área da região.
Encontre a área da região limitada pela parábola y = x 2 , pela reta tangente a essa parábola em 1 ,1 e pelo eixo x .
Suponha que 0cπ / 2 . Para qual valor de c a área da região limitada pelas curvas y = cos ⁡ x , y = cos ⁡ x - c e x = 0 é igual à área da região limitada pelas curvas y = cos ⁡ x - c , x = π e y = 0 ?