1. Aproxime por um polinômio de Taylor com grau em .
2. Use a desigualdade de Taylor para estimar a precisão da aproximação quando estiver no intervalo dado.
3. Verifique seu resultado na parte (b) traçando

(a) Vamos encontrar o polinômio de Taylor de grau 2 para centrado em .

A fórmula da série de Taylor é:

Para precisamos calcular até a segunda derivada de .

Calculando as derivadas e substituindo no centro :

Então o polinômio de Taylor de grau 2 é:

Substituindo os valores encontrados:

(b) Para usar a desigualdade de Taylor temos a seguinte relação, se , então

Então para estimar o erro, vamos precisar primeiramente da terceira derivada

Agora precisamos de um valor que seja maior que essa função em todo o intervalo , para isso podemos analisar o seguinte, em todo o intervalo a função de está crescente, porém é negativa, então em módulo para pegarmos o maior valor da função, precisamos do menor valor do intervalo () e substituirmos, podemos dizer que

Então podemos usar

Temos então que

Agora precisamos do valor de , se manipularmos o intervalo subtraindo em todas as partes da igualdade

Podemos colocar em módulo

Elevando ao cubo

Logo

(c) Traçando o gráfico de , para achar a função vamos usar a definição que diz

No plano

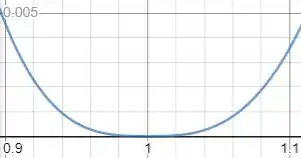
Pelo gráfico parece que o erro é menor que .