Um avião voa horizontalmente a uma altitude de km, a km/h, e passa sobre uma estação de radar. Encontre a taxa segundo a qual a distância entre o avião e a estação aumenta quando ele está a km além da estação.
(a) Quais são as quantidades dadas no problema?
(b) Qual é a incógnita?
(c) Faça um desenho da situação para qualquer instante .
(d) Escreva uma equação que relacione as quantidades.
(e) Termine a resolução do problema.
Passo 1
Opa, bora lá resolver mais uma questão! Temos um avião voando em uma altura a . Assim, visualmente, temos que:
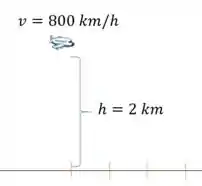
Ele passa por um radar e segue, queremos a taxa da distância entre o avião e o radar quando o avião esta depois do radar, ou seja:
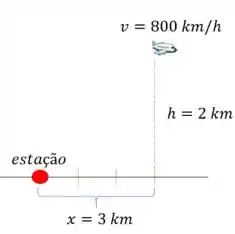
Mas antes, temos que responder alguns itens que o nosso enunciado pede!
O legal é que esses itens são o nosso passo a passo!! Quer ver?? Bora junto!!
😉
Passo 2
Item a: Quais são as quantidades dadas no problema?
As quantidades dadas do problema são os dados que temos, ou seja:
1) A altitude do avião (altura vertical): ;
2) A velocidade horizontal do avião: ;
3) A distância horizontal do avião em relação à estação de radar no momento de interesse: .
Item b: Qual é a incógnita?
A incógnita é o que queremos calcular, ou seja, é a taxa segundo a qual a distância entre o avião e a estação aumenta quando o avião está a além da estação, ou seja, .
Sendo que é a distância entre o avião e a estação.
Passo 3
Item c: Faça um desenho da situação para qualquer instante .
Opa, já temos (vamos apenas acrescentar o ):
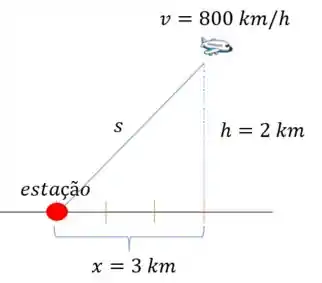
Note que temos um triângulo retângulo, onde:
1) Um cateto vertical representa a altitude do avião ;
2) O cateto horizontal representa a distância horizontal do avião em relação à estação ;
3) A hipotenusa representa a distância entre o avião e a estação.
Passo 4
Item d: Escreva uma equação que relacione as quantidades.
Como a situação descreve um triângulo retângulo, então o Teorema de Pitágoras se aplica:
Substituindo :
Passo 5
Item e: Termine a resolução do problema:
Queremos quando .
Dessa forma, substituindo na expressão anterior, obtemos:
Agora, derivando implicitamente equação com relação a , e já sabendo eu a derivada de uma constante é zero, obtemos:
Simplificando a expressão:
Substituindo pelos valores conhecidos, obtemos:
Ou, aproximadamente:
Resposta
a)
1) A altitude do avião (altura vertical): ;
2) A velocidade horizontal do avião: ;
3) A distância horizontal do avião em relação à estação de radar no momento de interesse: .
b)
A incógnita é a taxa segundo a qual a distância entre o avião e a estação aumenta quando o avião está a além da estação, ou seja, .
c)
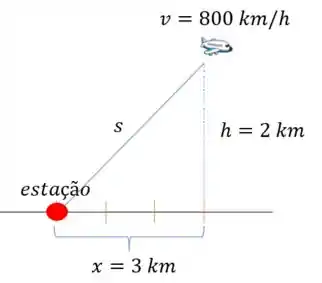
d)
e)