(a) Se forem emprestados a de juros, encontre as quantias devidas ao fim de três anos se os juros forem compostos () anualmente, () trimestralmente, () mensalmente, () semanalmente,() diariamente, () a cada hora ou () continuamente.

(b) Suponha que sejam emprestados e que os juros sejam capitalizados continuamente. Se for a quantia devida depois de anos, em que , trace para cada uma das taxas de juros , e em uma mesma tela.

Temos a taxa de juros de então , a quantia inicial é então e queremos saber o valor depois de anos, então, .

Desse modo obtemos a seguinte equação:

Agora para cada frequência de contabilização temos um deferente:

() anualmente: Os juros serão contabilizados uma vez por ano, então :

() trimestralmente: Os juros serão contabilizados quatro vezes por ano, então :

() mensalmente: Os juros serão contabilizados doze vezes por ano, então :

() semanalmente: Os juros serão contabilizados vezes por ano, então :

() diariamente: Os juros serão contabilizados vezes por ano, então :

() a cada hora: Os juros serão contabilizados por ano, então :

() continuamente: Os juros serão contabilizados infinitas vezes ao ano, logo, o valor de tende ao infinito. Portanto a quantia pode ser o limite:

Tranquilo até aqui?

Se tende ao infinito quando os juros são contabilizados continuamente, então temos a fórmula genérica para isso que é dada por:

Então para os juros de , e temos as respectivas funções:

Cuja representação gráfica é:

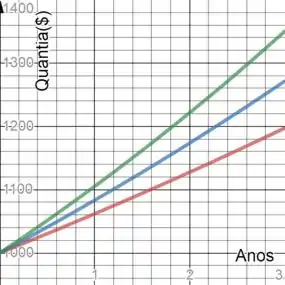
No gráfico a curva vermelha, a azul e a verde, correspondem aos juros de , e ,respectivamente.

É isso! O que achou? Responde Aí!