Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 13
13 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
O objetivo é encontrar todos os pontos críticos do sistema acima.
Agora, para os pontos críticos,
E,
Agora a equação implica que,
ou
E a equação implica que,
ou
Portanto, existem apenas três possibilidades, como mostrado abaixo:
A primeira possibilidade é quando, e então, isso implica que e .
A segunda possibilidade é, e então isso implica que e .
A terceira e a última possibilidade é, e então isso implica que .
Portanto, os pontos críticos são:
Passo 2
b) Observe que o gráfico de fase está no intervalo, conforme descrito abaixo:
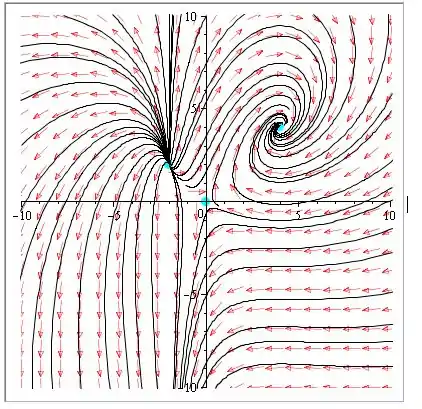
Passo 3
c)
Para o ponto crítico todas as trajetórias estão se afastando das soluções de equilíbrio, portanto, este é um ponto de sela instável.
Para o ponto crítico, é óbvio que todas as trajetórias são em forma de espiral e convergem para o ponto fixo, portanto, essa é uma espiral assintoticamente estável.
Para o ponto crítico, todas as trajetórias estão se afastando dos pontos fixos e parecem estar cruzadas lá, portanto, este é um nó Instável.
Passo 4
d) Por esta nota que, como existe apenas uma Espiral Assintoticamente Estável, portanto, a bacia de atração é .
Resposta
- pontos críticos
- O campo de direção é mostrado abaixo:
- O ponto crítico é um ponto de sela instável.
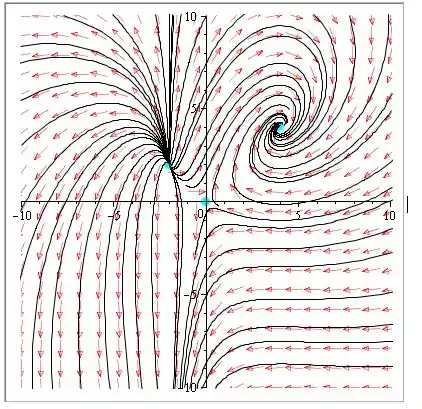
O ponto crítico é um ponto de espiral e assintoticamente estável.
O ponto crítico é um nó instável.
d) Por esta nota que, como existe apenas uma Espiral Assintoticamente Estável, portanto, a bacia de atração é .