Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 9
9 -
Passo 1
- As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Isso é,
Se temos
E se , então:
e
e
Portanto, os pontos críticos são:
Passo 2
b) Campo de direção do sistema fornecido:
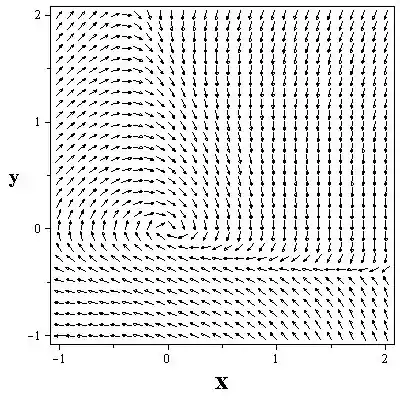
O retrato da fase para o sistema pode ser desenhado como abaixo:
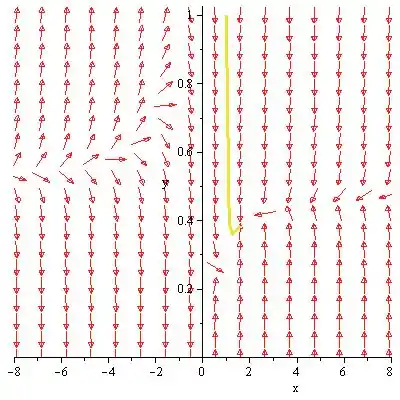
Passo 3
c) A partir das parcelas acima, podemos ver que o comportamento próximo à origem é o de uma espiral estável. Portanto, o ponto crítico é assintoticamente estável e, portanto, é afundado em espiral. No ponto crítico , as trajetórias se assemelham àquelas próximas a uma sela. Portanto, o ponto crítico é instável.
No ponto crítico , as trajetórias se assemelham àquelas próximas a uma sela. Portanto, o ponto crítico também é instável.
Passo 4
d) A bacia de atração de um ponto crítico assintoticamente estável é o conjunto de todos os pontos ao redor do ponto crítico a partir do qual a solução convergirá para o ponto crítico. Portanto, a partir do gráfico acima, a bacia de atração para o ponto crítico assintoticamente estável é o primeiro quadrante.
Resposta
- Os pontos críticos:
-
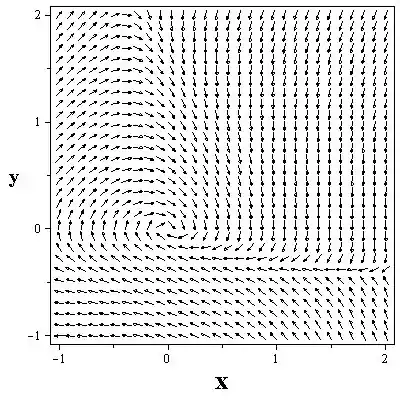
O retrato da fase para o sistema pode ser desenhado como abaixo:
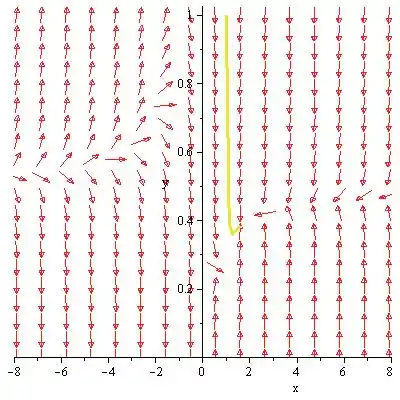
- O ponto crítico é um ponto de sela instável.
- A bacia de atração de um ponto crítico assintoticamente estável é o conjunto de todos os pontos ao redor do ponto crítico a partir do qual a solução convergirá para o ponto crítico. Portanto, a partir do gráfico acima, a bacia de atração para o ponto crítico assintoticamente estável é o primeiro quadrante.
O ponto crítico é o ponto de espiral e é assintoticamente estável.
O ponto crítico é um ponto de sela e instável.