Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.7 - Ex. 29
Para cada função velocidade dada:
- Gere a curva velocidade versus tempo e use-a para fazer uma conjectura sobre o sinal do deslocamento sobre os intervalos de tempo dados.
- Use um CAS para encontrar o deslocamento.
Passo 1
(a) A conjectura que ele fala para gente fazer é baseada nessa fórmulinha:
Ela diz que o deslocamento é a área líquida do gráfico da nossa curva no intervalo dado. Olhar a área líquida é dar sinal positivo para a parte da área acima do eixo e sinal negativo para a parte que estiver abaixo, e somar tudo algebricamente.
Então, para analisar o sinal do deslocamento, vamos analisar o sinal da área líquida. Vamos ver se a área acima do eixo é maior que a área abaixo do eixo (deslocamento positivo), menor (deslocamento negativo) ou igual (deslocamento nulo).
Vamos lá!
Passo 2
Vamos usar o Geobebra (dá para acessar pelo navegador mesmo) para gerar a curva:
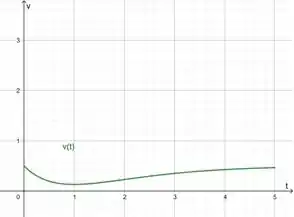
Dá para ver que área acima do eixo é maior do que a área abaixo, porque só tem área acima do eixo. Então a gente vai esperar um deslocamento positivo.
Passo 3
(b)Agora é só calcular integral:
Que com os nossos dados fica:
Usando o CAS do Geogebra (pelo navegador também):
Nossa estimativa estava certinha. Deu positivo.
Resposta
- Positivo