Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.8 - Ex. 3
Em cada um dos problemas de 1 a 4:
(a) Desenhe um campo de direções e esboce algumas trajetórias.
(b) Descreva como as soluções se comportam quando .
(c) Encontre a solução geral do sistema de equações.
Passo 1
Para (b). Faremos uma breve analise após o desenharmos as direções do campo e suas trajetórias, ou podemos calculara letra (c) e aplicaremos para tendendo a infinito e veremos o resultado deste limite ou analise gráfica.
Na letra (c) encontraremos os autovalores e autovetores da matriz e por final aplicaremos a formula da solução geral.
Passo 2
a) Direção do campo que possuimos: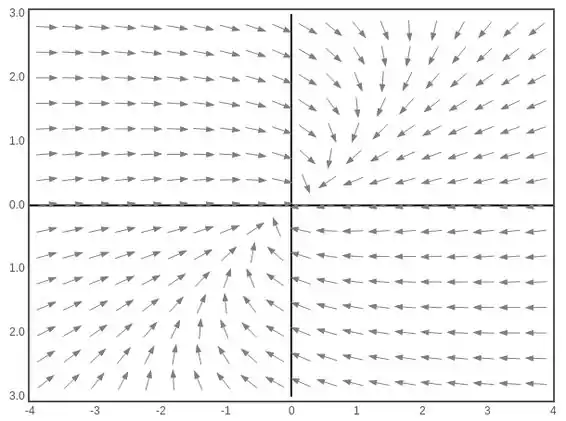
b) Acredito que fica bem tranquilo de enxergar no gráfico que para tendendo para infinito todo o campo converge para a origem.
Passo 3
c) Para determinarmos a solução geral do sistema temos que encontrar os autovalores e autovetores associados.
Para isto utilizaremos a seguinte relação:
Em que os autovalores serão as raízes do .
Determinando os autovalores:
Tendo as raízes:
Vamos agora determinar o autovetor associado, colocando , temos:
Escalonando a matriz temos:
Reduzindo o sistema para:
Para :
Para podermos calcular a segunda solução linear, teremos que generalizar um vetor próprio:
Escalonando a matriz temos:
Temos que:
Procuramos um vetor que satisfaça está equação, um deles pode ser:
Aplicando a segunda solução para autovalores repetidos:
Aplicando a formula da solução geral temos:
Logo a solução geral fica:
Resposta
b) Acredito que fica bem tranquilo de enxergar no gráfico que para tendendo para infinito todo o campo converge para a origem.
c)