Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.6 - Ex. 1
Em cada um dos problemas de a :
Expresse a solução geral do sistema de equações dado como combinação e de funções reais
Desenhe, também um campo de direções, esboce algumas trajetórias e descreva o comportamento das soluções quando
Passo 1
Descobrindo o valor dos autovalores desse sistema nós teremos:
Descobrindo os valores das raízes nós temos:
E como temos raízes complexas com parte real igual então nossa solução fica da seguinte maneira:
Sem nenhum valor de constante.
Passo 2
Para teremos o autovalor , ou seja:
Então pela multiplicação vetorial vemos que:
O que nos daria um auto vetor igual a:
Isso para a primeira linha já para a segunda:
Se substituirmos e como no autovetor encontrado na primeira linha nós teremos:
O que nos dá o resultado correto. Logo a solução para esse autovalor será:
Pois e
Pegando essa solução como solução geral do sistema nós vamos obter:
Passo 3
Plotando o campo de direções temos:
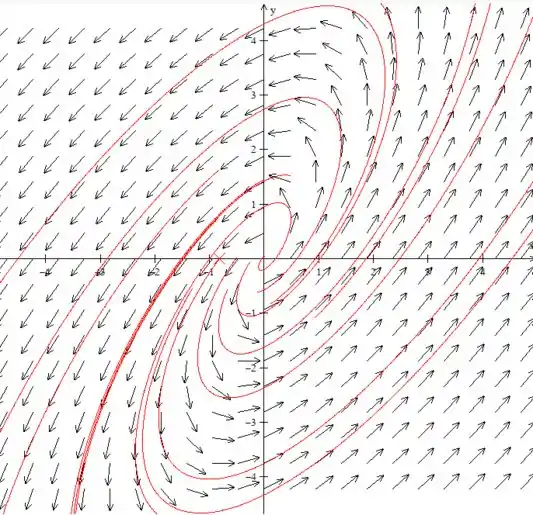
Eu acho mó daora esse tipo de gráfico hahaha . E ele vai tender para um valor muito grande para . Sendo um sistema instável, até ressonante.