Uma caixa de tampa deve ser construída a partir de um pedaço quadrado de papelão, com pés de largura, cortando fora um quadrado de cada um dos quatro cantos e dobrando para cima os lados. Encontre o aior volume que essa caixa poderá ter.

(a) Faça vários diagramas para ilsutrar a situação, algumas caixas pequenas com bases grandes e outras altas com base pequena. Encontre os volumes de várias dessas caixas. Parece existir um volume máximo? Se a resposta for sim, estime-o.

(b) Faça um diagrama ilustrando a situação geral. Introduza a notação e marque no diagrama seus símbolos.

(c) Escreva uma expressão para o volume.

(d) Use a informação dada para escrever uma equação que relacione as variáveis.

(e) Use a parte (d) para escrever o volume como uma função de uma só variável.

(f) Acabe de resolver o problema e compare sua resposta com a sua estimativa da parte (a).

Item a). Vamos começar fazendo desesnhos de dois tipos de caixas: uma alta a estreita, uma baixa e larga, e uma mais equilibrada. Todas elas vão ser recortadas de um papelão quadrado com pés de lado:

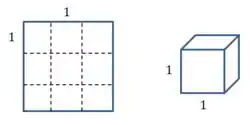
Essa caixa tem volume . Lembrando que é o símbolo para “pés”.

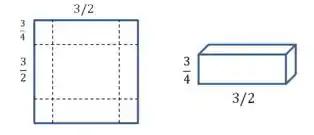
Essa caixa tem volume

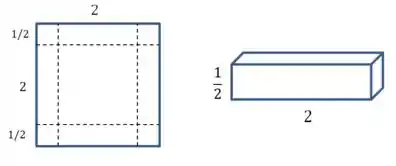
E essa caixa tem volume .

Então, pelas nossas simulações, o volume máximo deve ser de pelo menos pés cúbicos.

(b) Agora vamos fazer um diagrama que ilustre a situação geral:

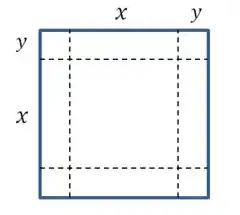
(c) Então a fórmula para o volume da caixa é:

(d) O enunciado diz que o lado do quadrado de onde a caixa é recortada mede pés.

Como não sabemos como a caixa será de fato dobrada, podemos escrever o seguinte:

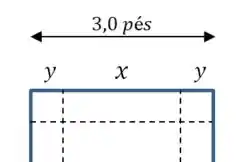
(d) E podemos usar isso para reescrever a nossa equação para o volume:

Já que o volume é dado por:

Teremos:

(e) Agora vamos encontrar os pontos extremos dessa função:

Podemos resolver essa equação do segundo grau:

E as duas raízes são e .

Vamos substituir na função para encontrar o volume associado a cada uma dessas raízes:

Começando pela raiz

E agora :

Então o valor máximo do volum é , o que coincide com a estimativa que fizemos no item (a).