Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 35
Calcular
Onde S é a superfície plana recortada pelo cone e pelo plano
Passo 1
A superfície que queremos é o plano formado pela curva abaixo e o plano .
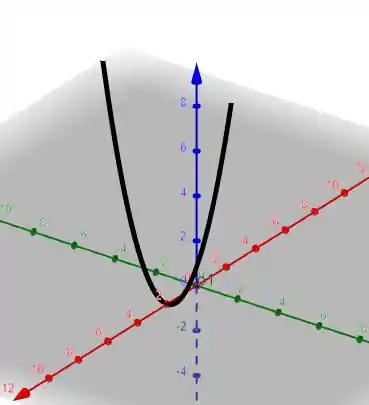
Isso Porque o cone faz no plano uma parábola. Logo para gente seria melhor projetar essa parte da parábola no plano
Logo nossa integral fica
Passo 2
A função x que vamos retirar as derivadas parciais é da equação do cone
Assim podemos escrever x como
Onde as parciais são
Passo 3
Vamos unir tudo na integral
Como nossa função , então não precisamos parametrizar. Apenas faríamos isso caso f dependesse de x.
Agora vamos definir os intervalos de integração. N afigura acima, vimos que no plano ZY temos uma parábola . Logo podemos escrever os intervalos de integração como
É sempre bom escolher bem a ordem de integração. NO nosso caso integrar primeiro em z faz sentido porque z cresce como uma função de y e para em . Restando para y intervalos numéricos.
Vamos terminar de integrar
Terminamos por aqui. Te vejo na próxima resolução
: )