Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.8 - Ex. 6
Calcular , sendo a região delimitada por e .
Passo 1
A representação da região de integração é dada:
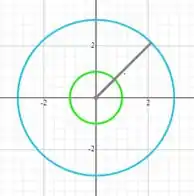
Assim:
e
Como:
; ;
Temos:
Desse modo, temos que:
Passo 2
As coordenadas polares se dão da seguinte forma:
; ;
Então, substituindo na equação dada, temos:
Passo 3
Integrando para :
Aplicando os limites:
Passo 4
Integrando para :
Aplicando os limites:
Resposta
Exercícios de Livros Relacionados
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}
Calcule a integral duplaint int_D (d x d y)/((p^2 + x^2 + y^2)^p) Onde: D = {(x , y) in R^2| x^2 + y^2 = a^2 } .
Se a0 , seja I a = ∫ - a a e - u 2 d u .Calcule as integrais sobre B 1 e B 2 , e use b ) para mostrar que I a tende para π quando a tende para + ∞ . Isto prova que ∫ 0 + ∞ e - u 2 d u = π 2 .