Calcular o volume do sólido delimitado por e
Passo 1
Bora começar?!
Então galera, a primeira coisa a fazer aqui é tentar desenhar:
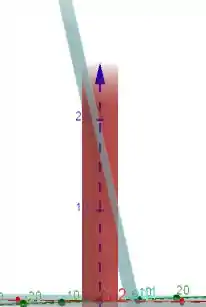
Para calcular o volume nós vamos precisar limitar z.
O z será definido por:
E:
Já o x nós teremos:
Obrigatoriamente:
Que nos dá:
Passo 2
Agora que já sabemos os intervalos de integração:
Resolvendo:
Sendo assim:
Resolvendo a integral:
Sabendo que:
Aplicamos o intervalo:
Então:
Vamos resolver cada integral separadamente.
Passo 3
Vamos começar por:
Chamando:
O novo intervalo será:
Aplicando na integral:
Aplicando a identidade:
Sabendo que:
Então:
Usando uma nova substituição:
Aplicando o intervalo:
Já resolvemos uma, agora só falta a segunda:
Chamando:
Substituímos u:
Aplicando o intervalo:
Então o resultado da nossa integral do Passo 2 será:
O que acharam desta?