Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 4.2 - Ex. 2a
Calcule
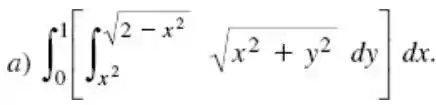
Passo 1
Neste caso, o conjunto deve ser determinado antes de tudo. Assim, visto que varia de a , para cada valor de fixo em , varia de a . Logo, conclui-se que essa região é o conjunto:
Dessa forma, vê-se que ele representa a região limitada por um círculo de raio e uma parábola. Então, fazendo:
Pretende-se determinar o resultado da transformação:
Dada por:
Então:
Portanto:
Passo 2
Agora, deve se determinar o conjunto , onde . Assim, o novo conjunto será dado através do limite do conjunto original. Visto que é mostrado no esboço a seguir:
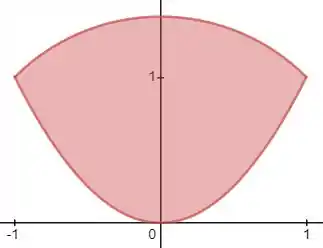
Então as novas variáveis serão dadas por:
Quando
Quando
Quando
Quando
E, como a região é definida por duas figuras diferentes, o intervalo será dividido em dois:
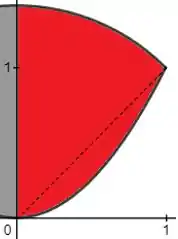
E
Dessa forma, tem-se:
Passo 3
Logo, mudando a variável na integral dupla:
E, resolvendo-a:
Substituindo o intervalo de integração:
Passo 4
Utilizando a identidade trigonométrica
Podemos reescrever:
Resolvendo a primeira integral pelo método da substituição com , tal que , então:
Então:
Substituindo o intervalo de integração: