Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.2 - Ex. 6a

Calcule f^' ( x ) , pela definição.

a ) f (x) = x^2 + x

Passo 1

Essa é uma parte HARD de Cálculo. Calcular pela definição é sempre mais complicadinho, mas nunca dá erro. Inclusive, as vezes os truques de derivação não dão certo, então seremos forçados a calcular pela definição. Treinar isso é importante. Então vamos arregaçar as mangas. Vamos relembrar que a definição de derivada f^' ( x ) é:

f^' (x) = underset(h -> 0)(lim) (f (x + h) - f ( x ))/(h)

Passo 2

Aqui temos que

f (x) = x^2 + x

e

f (x + h) = (x + h)^2 + ( x + h )

Então substituindo na definição temos:

f^' (x) = underset(h -> 0)(lim) ((x + h)^2 + (x + h) - x^2 - x)/(h)

Passo 3

Agora vamos abrir a parte quadrada do numerador:

f^' (x) = underset(h -> 0)(lim) (x^2 + h^2 + 2 x h + (x + h) - x^2 - x)/(h) =

underset(h -> 0)(lim) (h^2 + 2 x h + h)/(h) -> underset(h -> 0)(lim) (h ( h + 2 x + 1 ))/(h)

underset(h -> 0)(lim) h + 2 x + 1

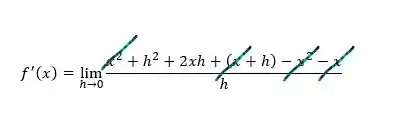
Agora nós vamos aplicar esse limite, quando h -> 0 o valor de f^' ( x ) é:

f^' (x) = 2 x + 1

Terminamos por aqui. Te vejo no próximo exercício: )

Resposta

f^' (x) = 2 x + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine todos os pontos x , y no gráfico de f x = x 2 com tangentes que passam pelo ponto ( 3,8 ) .
Para os Exercícios 67 e 68, avalie cada limite ao converter cada um deles em uma derivada com um determinado valor de x . lim x → - 1 ⁡ x 2 / 9 - 1 x - 1
Para os Exercícios 67 e 68, avalie cada limite ao converter cada um deles em uma derivada com um determinado valor de x . lim x → 1 ⁡ x 50 - 1 x - 1
Quantidade ideal de pedidos Uma das fórmulas para gerenciamento de estoque diz que o custo médio semanal de pedidos, pagamentos e armazenamento de mercadoria é A q = k m q + e m + h q 2 em que q é a q
Uma empresa estima que em t anos o número de seus empregados será N t = 1000 0,8 t 2 a ) Quantos empregados a empresa espera ter em 4 anos? b ) Com que taxa estará variando o número em 4 anos?