Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.3 - Ex. 7

Calcule as integrais nos Exercícios 1-14.

7.

int sqrt(25 - t^2)

Passo 1

O enunciado pede para gente calcular o valor dessa integral, para isso a gente vai usar algumas substituições trigonométricas.

Vamos usar essa imagem de referência

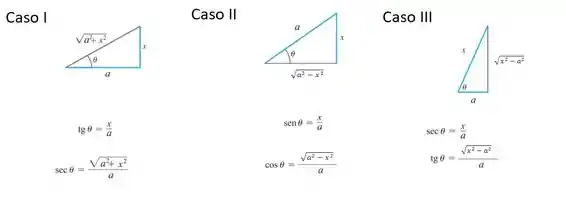
Esse caso se encaixa no caso II.

Passo 2

Vamos fazer uma substituição

t = 5 s e n ѳ d t = 5 cos ѳ d ѳ

E nossa integral fica o seguinte

int sqrt(25 - 25 s e n^2 ѳ) * 5 c o s ѳ d ѳ

Passo 3

Agora podemos colocar o 5 em evidência

int sqrt(25 - 25 s e n^2 ѳ) * 5 c o s ѳ d ѳ = int 5 sqrt(1 - s e n^2 ѳ) * 5 c o s ѳ d ѳ

Passo 4

Mas sabemos que

sqrt(1 - s e n^2 ѳ) = cos ѳ

Então

int 5 sqrt(1 - s e n^2 ѳ) * 5 c o s ѳ d ѳ = int 5 cos ѳ * 5 c o s ѳ d ѳ = 25 int c o s^2 ѳ d ѳ

Passo 5

Mas sabemos que

c o s^2 ѳ = (1 + cos 2 ѳ)/(2)

Então

25 int c o s^2 ѳ d ѳ = 25 int (1 + cos 2 ѳ)/(2) d ѳ = 25 * [int (1)/(2) d ѳ + int (cos 2 ѳ)/(2) d ѳ]

Passo 6

Agora é só calcular a integral

25 * [int (1)/(2) d ѳ + int (cos 2 ѳ)/(2) d ѳ] = 25 * [(1)/(2) ѳ + (1)/(2) * s e n ѳ * cos ѳ] + C

Passo 7

Mas sabemos que

t = 5 s e n ѳ

Então

ѳ = a r c s e n ((t)/(5))

Então nosso resultado fica

25 * [(1)/(2) a r c s e n ((t)/(5)) + (1)/(2) * s e n (a r c s e n ((t)/(5))) * cos (a r c s e n ((t)/(5)))] + C

Isso vai ficar

(25)/(2) * [a r c s e n ((t)/(5)) + ((t)/(5)) * (sqrt(25 - t^2))/(5)] + C

Resposta

(25)/(2) * [a r c s e n ((t)/(5)) + ((t)/(5)) * (sqrt(25 - t^2))/(5)] + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule.int x^2 (x + 1)^(10) d x
Calcule a área do conjunto de todos os (x , y) tais que 4 x^2 + y^2 = 1 .
Calcule.int (1)/(x^2 sqrt(1 + x^2)) d x
Calcule.int x^2 sqrt(x - 1) d x
Calcule.int sqrt(- x^2 + 2 x + 3) d x