Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.4 - Ex. 3a

Calcule as integrais, para as regiões D indicadas.

(a) int int_D y^2 s e n (x^2) d x d y ; D l i m i t a d a p o r y = x^(1 // 3) , y = - x^(1 // 3) e x = 8

Passo 1

E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D

Primeiro, vamos lembrar do Teorema de Fubini (que pode ser encontrado no livro DIOMARA - CÁLCULO DIFERENCIAL E INTEGRAL DE FUNÇÕES DE VÁRIAS VARIÁVEIS - 1 ª ED. (página 1 61 )) que diz que se a função z = f (x , y) for contínua em um retângulo R = [a , b] xx [c , d] , então:

int int_R f (x , y) d x d y = int_a^b [int_c^d f (x , y) d y] d x = int_c^d [int_a^b f (x , y) d x] d y

Para regiões não retangulares, a diferença é que apenas uma das integrais terá constantes no seu limite de integração, enquanto a outra integral terá funções no limite de integração. Isso é mostrado em:

int int_R f (x , y) d x d y = int_a^b [int_(c (x))^(d (x)) f (x , y) d y] d x = int_c^d [int_(a (y))^(b (y)) f (x , y) d x] d y

Como no nosso caso temos uma região do tipo 1 em que a região é contínua em x e possui y limitada por funções de x , temos que aplicar a inversão da ordem de integração do Teorema de Fubini.

Além disso precisamos definir o intervalo de integração de x .

Passo 2

Então, como queremos saber o intervalo de x vamos esboçar o gráfico dessa região. Temos que:

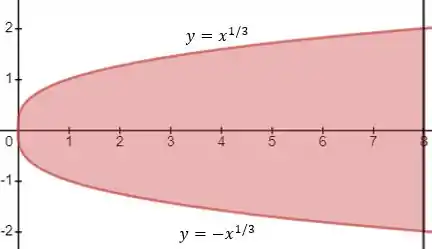
Podemos ver que os intervalos serão dados por:

- x^(1 // 3) <= y <= x^(1 // 3)

E:

0 <= x <= 8

Passo 3

Dessa forma, podemos escrever:

int_0^8 int_(- x^(1 // 3))^(x^(1 // 3)) y^2 s e n (x^2) d y d x = int_0^8 s e n (x^2) int_(- x^(1 // 3))^(x^(1 // 3)) y^2 d y d x

Então, resolvendo a integral interna:

int_0^8 s e n (x^2) int_(- x^(1 // 3))^(x^(1 // 3)) y^2 d y d x = int_0^8 s e n (x^2) [(y^3)/(3)] | [[x^(1 // 3)],[-,x^(1 // 3)]] d x

Substituindo o intervalo de integração da integral resolvida:

=> (1)/(3) int_0^8 s e n (x^2) [(x^((1)/(3)))^3 - (- x^((1)/(3)))^3] d x

O que resulta em:

=> (1)/(3) int_0^8 s e n (x^2) [x - (- x)] d x = (2)/(3) int_0^8 x s e n (x^2) d x

Passo 4

Logo, podemos resolver essa integral pelo método da substituição simples usando u = x^2 e d u = 2 x d x , tal que:

Quando x = 0 -> u = 0 ;

Quando x = 8 -> u = 64

Dessa forma:

(2)/(3) int_0^8 x s e n (x^2) d x = (2)/(3) int_0^(64) s e n (u) ((d u)/(2))

Ou seja:

=> (1)/(3) int_0^(64) s e n (u) d u = (1)/(3) [- cos u] | | [[64],[0]]

E substituindo o intervalo de integração:

=> - (1)/(3) (cos 64 - cos 0) = (1)/(3) - (1)/(3) cos 64

Que pode ser reescrito como:

=> (1)/(3) (1 - cos 64)

Resposta

(1)/(3) (1 - cos 64)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As integrais abaixo não podem ser calculadas exatamente, em termos de funções elementares, com a ordem de integração dada. Inverta a ordem de integração e faça os cálculos. b∫ 0 1 ∫ x 1 s e n y y d y
Determine a região de integração D e troque a ordem de integração das seguintes integraisa. ∫ 0 1 ∫ x 3 x f x , y d y d x
Determine a região de integração D e troque a ordem de integração das seguintes integraisb. ∫ 0 1 ∫ - 1 - y 2 1 - y f x , y d x d y
Determine a região de integração D e troque a ordem de integração das seguintes integraisc. ∫ 0 π 2 ∫ cos ⁡ x 1 f x , y d y d x
2. AS integrais abaixo não podem ser calculadas exatamente, em termos de funções elementares, com a ordem de integração dada. Inverta a ordem de integração e faça os cálculosa. ∫ 0 1 ∫ y 1 e x 2 d x d