Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 11
Calcule a integral dada, colocando-a em coordenadas polares.
onde é a região delimitada pelo semicírculo e o eixo .
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!
Para resolver essa questão, primeiro vamos esboçar a região para visualizá-la melhor. O enunciado nos fornece a equação . Reorganizando os termos, obtemos
De acordo com a teoria das coordenadas polares, a equação:
representa a equação de uma circunferência de raio 2, , centrada na origem.
MAAASSS como nem tudo é um mar de rosas, quando o enunciado diz , ele na verdade quer dizer , ou seja, queremos somente a parte positiva do eixo , a região será o semicírculo superior.
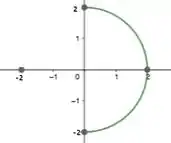
Passo 2
Agora que a gente já sabe a região, podemos definir as substituições e os intervalos. Temos então que
O nosso ângulo vai estar variando de acordo com a região D, dado o círculo trigonométrico
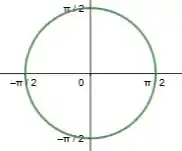
E a região
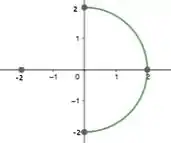
Temos então que os intervalos onde nossos valores estão variando são
Passo 3
Agora sim podemos escrever nossa integral em coordenadas polares
Temos então que
Lembrando que quando a substituição é para coordenadas polares, .
Então a integral se torna:
Passo 4
Vamos resolver a integral interna primeiro. Usando a substituição , temos que ou :
Integrando, obtemos:
Substituindo de volta na integral externa:
Esta integral é constante em relação a :
Calculando o valor da integral externa:
Então, substituindo de volta:
Ala ela, a cara do coisa ruim, isso quer dizer que
