Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.6 - Ex. 12
Calcule a integral tripla.
Onde está abaixo do plano e acima da região triangular com vértices , e .
Passo 1
Oii, tudo certo? Vamos dar uma olhada nessa questão:
Ela pede pra gente calcular uma integral tripla:
Sobre essa região que ele descreveu.
Então a primeira coisa que vamos fazer pra resolver é entender como é essa região, pra descobrir os limites de cada uma das variáveis , , e , e conseguir reescrever nossa integral como uma integral iterada.
Pra fazer isso, a gente vai escrever como uma região do tipo :
Ou seja, está entre duas funções de e , e estão em um domínio no plano – que é a projeção de .
Por último, vamos resolver a integral iterada, sempre de dentro pra fora!
Passo 2
Vamos começar olhando pra região : abaixo do plano e acima da região triangular com vértices , e .
De cara, a questão já disse que , porque a região está abaixo de .
Além disso, tá acima dessa região triangular. Só que percebeu que o valor de nos três vértices é ? Ou seja, a região tá acima de uma superfície em :
Então
Essa região é o interior do triângulo, que está no plano :
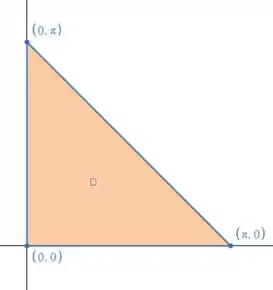
Pra definir os limites de e , vamos descobrir quem é essa reta que liga e .
Em uma reta do tipo , o coeficiente linear é o valor onde a reta corta o eixo , nesse caso, . O coeficiente angular calculamos assim:
Então:
Como o nesse domínio varia de até essa reta,
E o varia de até .
Então temos os limites das nossas três variáveis:
E assim a gente consegue reescrever nossa integral como uma integral iterada. Só lembrando que como os limites de e dependem de , o vai ser a última variável a ser integrada:
Passo 3
Começamos integrando em função de , considerando e como constantes:
Como é constante, o pode sair dessa integral, e fica:
Resolvendo os limites de integração:
Passo 4
Agora integramos em função de , considerando constante:
O pode sair dessa integral, e resolvemos:
Substituindo nos limites:
Passo 5
Por último, integramos em função de :
Vamos reescrever , usando a propriedade:
Então
Mas e , então
Voltando para a integral:
Podemos fazer uma distributiva, e separar em duas integrais:
A segunda integral vamos integrar por partes:
Então:
Voltando pra integral:
Resolvendo a primeira integral:
Agora é só substituir nos limites de integração:
Como , e , resolvemos:
Então a integral vale: