Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 51

Calcule a integral trocando a ordem de integração.

51.

∫ 0 1   ∫ 3 y 3 e x 2 d x d y

Passo 1

Oi, pessoal. Tudo belê?

A questão nos pede pra trocar a ordem de integração da integral, ou seja, em vez de resolver d x e depois d y , ela quer primeiro resolvido d y e depois d x . Moleza?

Primeiramente vamos encontrar a região, de acordo com os limites de integração:

D = { ( x , y ) ∣ 3 y ≤ x ≤ 3 ,   0 ≤ y ≤ 1 }

Esboçando o gráfico, ficaria assim:

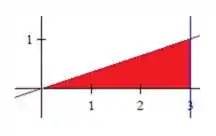
Invertendo a ordem de integração, temos que x vai de 0 até 3, enquanto y vai do eixo x ( y = 0 ) até a reta y = x 3 .

Assim, ó:

D = { ( x , y ) ∣ 0 ≤ y ≤ x 3 ,   0 ≤ x ≤ 3 }

Então, vamos inverter a ordem:

∫ 0 3   ∫ 0 x 3 e x 2 d y d x

Passo 2

Resolvendo a integral de dentro, temos:

∫ 0 x 3 e x 2 d y = y e x 2 0 x 3

= [ x 3 e x 2 - 0 e x 2 ]

Portanto:

x 3 e x 2

Passo 3

Vamos resolver a nova integral:

∫ 0 3   x 3 e x 2 d x

Aplicando a integração por substituição:

u = e x 2

d u d x = 2 x e x 2

d x = d u 2 x e x 2

Voltando a nossa integral e cancelando alguns termos::

∫ 0 3   x 3 e x 2 d u 2 ⋅ x ⋅ e x 2

∫ 0 3   1 3 ⋅ d u 2 =   ∫ 0 3   1 6 d u

Colocando essa fração pra fora da integral, resolvemos tudo numa boa!

1 6 ⋅ ∫ 0 3   d u

1 6 ⋅ u 0 3

Como u = e x 2 , então:

1 6 ⋅ e x 2 0 3

Substituindo os limites de integração:

1 6 e 3 2   - 1 6 ⋅ e 0 2

1 6 e 9   - 1 6 ⋅ e 0

e 9 6   - 1 6 = e 9 - 1 6

Resposta

∫ 0 3   ∫ 0 x 3 e x 2 d y d x = 1 6 e 9 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 1 ∫ 4 x 4 f x , yd y d x
Esboce a região de integração e mude a ordem de integração. ∫ 0 4 ∫ 0 x f x , yd yd x
Nos Exercícios 1-12, calcule a integral iteradaint_(pi)^(2 pi) int_0^(pi) ( s e n x + c o s y ) d x d y
Nos Exercícios 1-12, calcule a integral iteradaint_(- 1)^2 int_0^(pi // 2) y s e n x d x d y
É possível calcular a integral de uma função contínua f ( x , y ) sobre uma região retangular no plano x y e obter respostas diferentes dependendo da ordem de integração? Justifique sua resposta.