Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.2 - Ex. 52

Calcule a integral trocando a ordem de integração.

52.

∫ 0 1   ∫ x 2 1 y sin ⁡ y d y d x

Passo 1

Oi, pessoal. Tudo bem?

A questão nos pede pra trocar a ordem de integração da integral, ou seja, em vez de resolver d y e depois d x , ela quer primeiro resolvido d x e depois d y . Show?

O primeiro passo é analisar os limites de integração:

D = { ( x , y ) ∣ x 2 ≤ y ≤ 1 ,   0 ≤ x ≤ 1 }

Se quiser esboçar a região, respeitando os limites que foram dados, então encontramos a região D que vamos trabalhar:

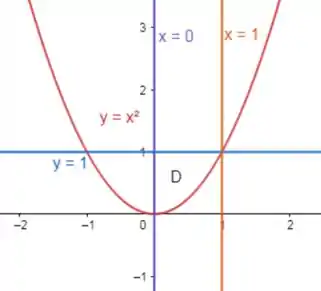
Invertendo a ordem de integração, temos que x vai de 0 até y , enquanto y vai do eixo x ( y = 0 ) até a reta y = 1 .

Assim:

∫ 0 1   ∫ x 2 1 y sin ⁡ y d y d x = ∫ 0 1   ∫ 0 y y   s e n y d x d y

Passo 2

Resolvendo a integral de dentro, temos:

∫ 0 y y sin ⁡ y d x

y   s e n y ⋅ x 0 y

y   s e n y ⋅ y - y   s e n y ⋅ 0

y 2   s e n y - 0

Tiramos a raiz, já que temos um expoente 2 dentro, e descobrimos a integral interna:

∫ 0 y y sin ⁡ y d x = y   s e n ( y )

Portanto:

∫ 0 1   ∫ 0 y y   s e n y d x d y = ∫ 0 1   y   s e n ( y ) d y

Passo 3

A nossa integral agora tem uma mistureba de coisas: um polinômio e uma função trigonométrica, percebe?

∫ 0 1   y   s e n ( y ) d y

Então vamos utilizar a técnica de integração chamada Integração por Partes, que tem essa fórmula aqui:

∫ u d v = u v - ∫ v d u

Vou chamar

u = y

d v = s e n y d y

Assim teremos:

d u = d y

v = - c o s ⁡ ( y )

Jogando esses carinhas na fórmula, temos:

y ⋅ [ - cos ⁡ y ] - ∫ - c o s ⁡ ( y ) d y

- y ⋅ cos ⁡ y + ∫ cos ⁡ y d y

- y ⋅ cos ⁡ y + s e n y 0 1

- 1 cos ⁡ 1 ⋅ s e n 1 - - 0 cos ⁡ 0 ⋅ s e n 0

Assim, encontramos nossa resposta:

s e n 1 - cos ⁡ 1

Resposta

∫ 0 1   ∫ 0 y y   s e n y d x d y = s e n 1 - cos ⁡ 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região de integração e mude a ordem de integração. ∫ 0 3 ∫ - 9 - y 2 9 - y 2 f x , y d x d y
Esboce a região de integração e mude a ordem de integração. ∫ 0 3 ∫ 0 9 - y f x , yd x d y
Calcule a integral trocando a ordem de integração. ∫ 0 1 ∫ 3 y 3 e x 2d xd y
Calcule a integral trocando a ordem de integração. ∫ 0 π ∫ y π cos ⁡ x 2d xd y
Calcule a integral trocando a ordem de integração. ∫ 0 4 ∫ x 2 1 y 3 + 1d yd x