Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.7 - Ex. 10

10. Calcule

∮ c - y x 2 + y 2 d x + x x 2 + y 2 d y

Onde C é a curva definida por

y 2 = 2   x + 2

- 2 ≤ x ≤ 2

orientada no sentido descrente de y

Passo 1

Oii, estamos ingressando no mundo dos teoremas de integração de cálculo. E nessa parte da matéria temos que aprender que existem muitas respostas diferentes utilizando caminhos diferentes como é neste caso de integração de linha. OU várias formas de se calcular que geram o mesmo resultado!

Sim, você ouviu certo. Vão ter contas que podemos fazer por ate 3 caminhos diferentes. Então a pergunta é : qual escolher? Segue vendo as nossas resoluções que vamos te dar umas dicas.

Passo 2

Neste capítulo trabalhamos conceitos de funções vetoriais, Teorema de Green e Campo conservativo. Vamos ter que lançar mãos de tudo isso para resolver nossas questões. Bora fazer uma revisão de leve nos teoremas. O Teorema de Green diz

∮ c F 1 d x + F 2 d y   = ∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d x d y  

Outra forma de enxergar seria

∮ c F ⋅ d r   = ∫ ∫ R ∇ × F d x d y  

Quando nosso campo é conservativo, acontece que

∇ × F = 0

Podemos fazer o rotacional e descobrir isso, ou por uma simples propriedade de diferenciação saber que

∇ × ∇ U = 0

e quando o nosso campo é conservativo podemos dizer que existe uma função Potencial U, de forma que

∇ U = F

Beleza? É bom fazer essa revisãozinha pra a gente já chegar afiado nas questões!!!!

Passo 3

Nesta questão temos essa curva

y 2 = 2   x + 2

- 2 ≤ x ≤ 2

Graficamente podemos ver ela abaixo

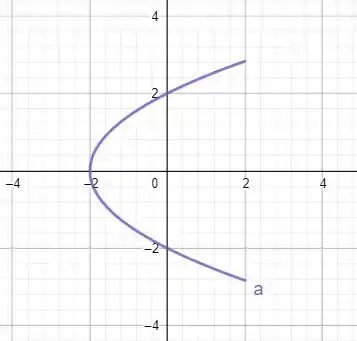
Temos um problema, temos que fazer essa integral de linha

∮ c - y x 2 + y 2 d x + x x 2 + y 2 d y

É um calculo muito complicado pra se fazer. Logo vamos usar o teorema de green. Contudo O teorema de green exige que seja uma curva fechada, temos que fazer uma segunda curva para fechar a região

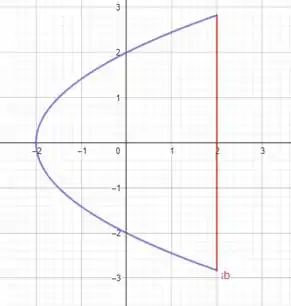
Entao o teorema de green sera

∮ c 1 F 1 d x + F 2 d y   +   ∮ c 2 F 1 d x + F 2 d y   = ∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d x d y  

A primeira coisa a se fazer é testar se

∂ F 2 ∂ x - ∂ F 1 ∂ y = 0

O que faz a nossa vida ser muito mais fácil. Vamos calcular essas derivadas parciais

∂ F 1 ∂ y = - x 2 + y 2 + 2 y 2 x 2 + y 2 2

∂ F 2 ∂ x = x 2 + y 2 - 2 x 2 x 2 + y 2 2

Logo

x 2 + y 2 - 2 x 2 x 2 + y 2 2 - - x 2 + y 2 + 2 y 2 x 2 + y 2 2 = 0

∂ F 2 ∂ x - ∂ F 1 ∂ y = 0

Isso funciona apenas se

x , y ≠ 0,0

Beleza, então nosso problema agora se resume a

∮ c 1 F 1 d x + F 2 d y   +   ∮ c 2 F 1 d x + F 2 d y   = 0

∮ c 1 F 1 d x + F 2 d y   = -   ∮ c 2 F 1 d x + F 2 d y  

Contudo nossa região compreende a origem. Logo temos que recortar essa região. Faremos um circulo ao redor do ponto 0,0 com um raio bem pequeno para que não influencie no nosso calculo

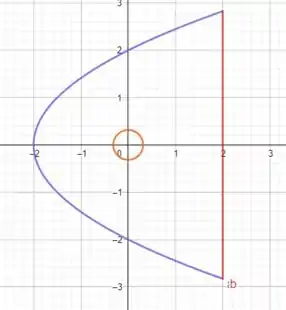
Uma maneira de calcular uma integral de linha é fazer o seguinte calculo

∮ c F ⋅ d r   =   ∮ c F γ t ⋅ γ ' ( t ) d t  

OU seja, parametrizar nossa função, então vamos encontrar a parametrização

γ t = r cos ⁡ t ,   r sen ⁡ t

γ ' t = - r sen ⁡ t ,   r cos ⁡ t

Vamos parametrizar nossa função

F x , y = - y x 2 + y 2 , x x 2 + y 2

F γ t = - r sen ⁡ t r 2   , r cos ⁡ t r 2

F γ t = - sen ⁡ t r   , cos ⁡ t r

Com isso nossa integral fica

=   ∮ c F γ t ⋅ γ ' t d t  

=   ∮ c - sen ⁡ t r   , cos ⁡ t r ⋅ - r sen ⁡ t ,   r cos ⁡ t d t  

=   ∮ c 1 d t  

Como esse circulo é fechado, o intervalo de t é 0,2 π

∮ 0 2 π d t = 2 π  

Passo 4

Entao ate agora nossa solução esta assim

∮ c 1 F 1 d x + F 2 d y   = 2 π -   ∮ c 2 F 1 d x + F 2 d y  

Vamos calcular agora essa curva C2. Vamos encontrar uma parametrização para ela

∮ c 2 F 1 d x + F 2 d y   =   ∮ c 2 F ⋅ d r   =   ∮ c 2 F γ t ⋅ γ ' ( t ) d t  

r =   γ t = 2 , t

d r = γ ' t d t = 0,1 d t

t ∈ - 8 , 8

Com isso nossa parametrização fica

F x , y = - y x 2 + y 2 , x x 2 + y 2

F γ t = - t 2 2 + t 2 , 2 2 2 + t 2

Com isso nossa integração fica

=   ∮ c 2 F γ t ⋅ γ ' t d t  

=   ∮ - 8 8 - t 2 2 + t 2 , 2 2 2 + t 2 ⋅ 0,1 d t

=   ∮ - 8 8 2 2 2 + t 2 d t

= 2 4   ∮ - 8 8 1 1 + t 2 2 d t

= 1 2   ∮ - 8 8 1 1 + t 2 2 d t

Fiz apenas uma pequena manipulação para deixar mais evidente que temos em mãos uma integral cuja primitiva é uma função trigonométrica. Você ouviu bem, não há truques. Apenas pegar a tabela e substituir os valores

1 2   ∮ - 8 8 1 1 + t 2 2 d t = 1 2   4 arctan ⁡ 2

= 2 arctan ⁡ 2  

UFAAA!!! Terminamos. Com isso nossa resposta final é

∮ c - y x 2 + y 2 d x + x x 2 + y 2 d y =   2 π - 2 arctan ⁡ 2

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

∮ c - y x 2 + y 2 d x + x x 2 + y 2 d y =   2 π - 2 arctan ⁡ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule cada uma das seguintes integrais ao longo da curva
Nos Exercícios 7-12, encontre as integrais de linha de F entre (0, 0, 0) e (1, 1, 1) sobre cada um dos seguintes caminhos da figura a seguir.c. O caminho C3 U C4 que consiste no segmento de reta de (0
Encontre os campos gradientes das funções nos Exercícios 1-4. g ( x , y , z ) = e z - l n ⁡ x 2 + y 2
Encontre os campos gradientes das funções nos Exercícios 1-4. f ( x , y , z ) = x 2 + y 2 + z 2 - 1 / 2
Dê uma fórmula F = M(x, y)i + N(x, y)j para o campo vetorialno plano que tem a propriedade de F apontar na direção da origem com magnitude inversamente proporcional ao quadradoda distância de (x, y) à