Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 6e

Calcule int int_B f (x , y) d x d y sendo dados:

Passo 1

Chamando a integral dupla do teorema de Fubini de F :

F = int int_B f (x , y) d x d y

Podemos reescrevê-la como:

F = int int_B (x + y) d x d y

Ou:

F = int_a^b [int_(c (y))^(d (y)) (x + y) d x] d y = int_c^d [int_(a (x))^(b (x)) (x + y) d y] d x

A partir do esboço do conjunto B :

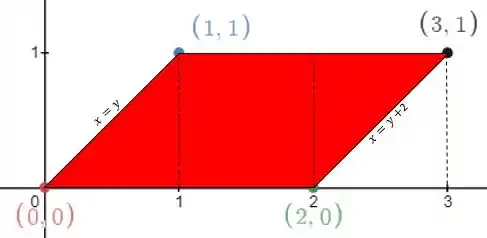
Pode-se observar que, devido à variação do valor da variável x , a figura pode ser separada ao meio, onde a equação das retas (que representam os lados do triângulo) se altera. Ainda, como o valor de x tem maior variação, torna-se mais conveniente deixá-lo em função da outra variável e manter y com variação constante.

Conclui-se, então, que os intervalos serão:

y <= x <= y + 2

E

0 <= y <= 1

Passo 2

Assim, é possível calcular:

F = int_0^1 [int_(x = y)^(x = y + 2) (x + y) d x] d y

F = int_0^1 [x y + (x^2)/(2)] | [[x,=,y,+,2],[x,=,y]] d y

Substituindo o intervalo de integração em x :

F = int_0^1 [(y + 2) y + ((y + 2)^2)/(2) - y^2 - (y^2)/(2)] d y

F = int_0^1 [4 y + 2] d y

Passo 3

Agora, integrando em relação a y :

F = [2 y^2 + 2 y] | [[y,=,1],[y,=,0]]

E, substituindo o intervalo de integração:

F = [2 + 2 - 0]

F = 4

Resposta

4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume sob o cilindro parabolico z = x 2 acima da região delimitada pela parabola y = 6 - x 2 e a reta y = x no plano xy.
Encontre o volume sob o paraboloide z = x 2 + y 2 acima do triangulo delimitado pelas retas y = x, x = 0 e x + y = 2 no plano xy.
Calcule int_0^a int_0^b e^(max (b^2 x^2 , a^2 y^2)) d y d x Onde a e b são números positivos e max (b^2 x^2 , a^2 y^2) = {[[b^2 x^2 s e b^2 x^2 = a^2 y^2],[a^2 y^2 s e b^2 x^2a^2 y^2]])
Quadrado ƒ(x, y) = 1/(xy) sobre o quadrado 1 ≤ x ≤ 2,1 ≤ y ≤ 2
Retângulo ƒ(x, y) = y cos xy sobre o retângulo 0 ≤ x ≤ p,0 ≤ y ≤ 1