Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 5d

Calcule int int_B y d x d y onde B é o conjunto dado.

Passo 1

Chamando a integral dupla do teorema de Fubini de F :

F = int int_B y d x d y

Ou:

F = int_a^b [int_(c (y))^(d (y)) y d x] d y = int_c^d [int_(a (x))^(b (x)) y d y] d x

E fazendo o desenho do conjunto B :

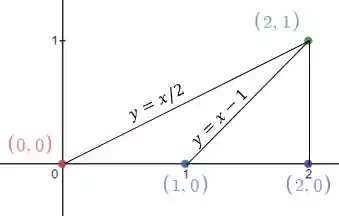
Para determinar o resultado do triângulo desejado, é possível fazer isso através da subtração dos triângulos formados pelos vérticas (0 , 0) , (2 , 0) , ( 2 , 1 ) e (1 , 0) , (2 , 0) , ( 2 , 1 ) . Dessa forma, se torna necessário o cálculo de duas integrais duplas, uma para cada um desses triângulos, tal que os intervalos de integração pro triângulo maior são:

0 <= x <= 2 e 0 <= y <= x // 2

E pro triângulo menor são:

1 <= x <= 2 e 0 <= y <= x - 1

Passo 2

Assim, é possível calcular para o triângulo maior:

F_1 = int_0^2 [int_0^(y = x // 2) y d y] d x

F_1 = int_0^2 [(y^2)/(2)] | [[y,=,x,//,2],[y,=,0]] d x

Substituindo o intervalo de integração em y :

F_1 = int_0^2 (1)/(2) [(x^2)/(4)] d x

Passo 3

Agora, integrando em relação a x :

F_1 = (1)/(8) [(x^3)/(3)] | [[2],[0]]

E, substituindo o intervalo de integração:

F_1 = (1)/(3) - 0 = (1)/(3)

Passo 4

Agora, para o triângulo menor:

F_2 = int_1^2 [int_0^(y = x - 1) y d y] d x

F_2 = int_1^2 [(y^2)/(2)] | [[y,=,x,-,1],[y,=,0]] d x

Substituindo o intervalo de integração em y :

F_2 = int_1^2 (1)/(2) [(x - 1)^2] d x = int_1^2 (1)/(2) [x^2 - 2 x + 1] d x

Passo 5

Agora, integrando em relação a x :

F_2 = (1)/(2) [(x^3)/(3) - x^2 + x] | [[2],[1]]

E, substituindo o intervalo de integração:

F_2 = (1)/(2) [(8)/(3) - 4 + 2 - ((1)/(3) - 1 + 1)] = (1)/(6)

Passo 6

Por fim, resta calcular a subtração citada no início da resolução. Logo:

F = F_1 - F_2 = (1)/(3) - (1)/(6)

F = (1)/(6)

Resposta

(1)/(6)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As integrais e somas de integrais nos Exercícios 13-18 fornecem as áreas das regiões no plano xy. Esboce cada região, marque cada curva limitante com sua equação e forneça as coordenadas dos pontos on
Encontre a altura média do paraboloide z=x 2+y 2 sobre o quadrado 0≤x≤2 ,0≤y≤2 .
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. ap a r a b o l ax = - y 2ear e t
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. A sr e t a sy = 2 x,y = x 2ey =
Nos Exercícios 1-12, esboce a região delimitada pelas retas e curvas dadas. Em seguida, expresse a área da região como uma integral dupla iterada e calcule a integral. a sr e t a sx = 0 ,y = 2 x ,ey =