Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 76
Uma calha deve ser construída com uma folha de metal de largura dobrando-se para cima da folha de cada lado, fazendo um ângulo com a horizontal. Como deve ser escolhido de forma que a capacidade de carregar água da calha seja máxima?
Passo 1
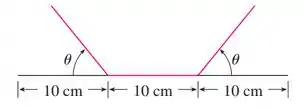
Opa! Bora pra mais uma questão?! Temos aqui um problema de maximização de área. O enunciado pede pra a gente calcular o ângulo de modo que a capacidade de uma calha seja máxima. Se liga nessa imagem:
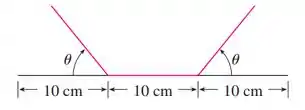
Ué, mas não seria uma maximização de volume?!
Sim, mas nesse caso a área da base vai ser constante, então podemos considerar apenas a área transversal da calha. Beleza?
Nesse problema vamos ter que escrever uma expressão que nos de a área em função de e deriva-la para achar onde é máximo. Vamos colocar a mão na massa?!
Passo 2
O que temos aqui é um trapézio, sua área é dada por:
Para achar uma relação da área com vamos dividir o trapézio em dois triângulos iguais e um retângulo, assim:
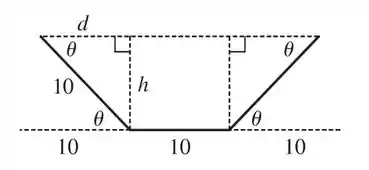
Dessa forma podemos dizer que:
Além disso:
Substituindo:
Passo 3
A fórmula que queremos maximizar é a seguinte:
Para isso vamos calcular :
Sabendo que:
Rearranjando e igualando a zero:
Ou:
Mas lembra do nosso intervalo? , então vamos excluir esse resultado.
Passo 4
Fazendo o teste da derivada com os valores extremos e :
Visto isso, a área máxima será quando .