Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.7 - Ex. 34
Uma cerca de de altura corre paralela a um edifício alto, a uma distância de do edifício. Qual o comprimento da menor escada que vai atingir do chão, por cima da cerca, à parede do prédio?
Passo 1
E aí, galerinha!
Nesse problema temos a seguinte situação: Temos um prédio bem alto e a desse prédio tem uma cerca de de altura. Uma escada é apoiada no prédio e no chão e passa por cima da cerca...
A partir daí queremos descobrir qual é o menor comprimento possivel para a escada a partir dessas condições.
Tem ideia de como fazemos isso?
Vamos começar esboçando o problema para ver o que podemos concluir...
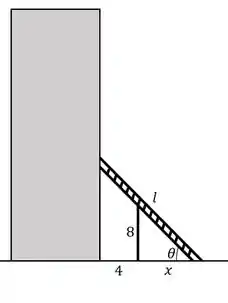
Claramente temos um problema de maximização e o que podemos fazer é representar o comprimento a partir de uma função de e .
E para minimizar a função temos que usar a ideia de pontos críticos, ou seja, derivar e igualar a . Mas pra isso temos que representar em função de uma única variável.
Veja só!
Passo 2
O comprimento se relaciona com e da seguinte maneira:
O segredo é eliminar uma das variáveis para poder minimizar a função.
Podemos eliminar a variavel e olharmos para o triangulo menor
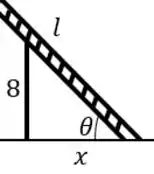
Ou seja, podemos relacionar e pela regra da tangente...
Então substituindo em , temos
Temos que lembrar que , e
Tranquilo até aqui?
Passo 3
A pior parte já foi, agora temos que derivar e igualar a ...
Pelo teorema fundamental do calculo temos que e
A função existe para todo , então devemos ter :
Lembra do passo anterior quando vimos que , e ? Então... vamos usar essas relações novamente e ainda vamos aplicar uma nova .
Veja só!
A partir da relação da tangente podemos simplificar essa equação como
Para afirmar que temos para esse valor de o mínimo absoluto da função, podemos dizer que é uma função contínua no intervalo e esse é o único ponto crítico dela, sendo que nos extremos, e , a função tende a mais infinito.
Show?
Passo 4
Agora devemos calcular o comprimento para esse ângulo . Temos:
Sabemos a tangente do ângulo, e queremos encontrar a secante e a cossecante.
Como Fazemos isso a partir de um triângulo retângulo que tem o ângulo :
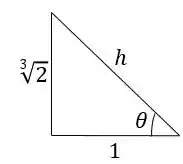
A hipotenusa é encontrada por Pitágoras:
Então achamos e relacionando com :
Finalmente, substituindo em , temos
E aí! o que achou? Responde Aí!