Considere a seguinte lista de equações diferenciais, algumas das quais produziram os campos de direção ilustrados nas figuras de 1.1.5 a 1.1.10. Em cada um dos problemas de 15 a 20, identifique a equação diferencial que corresponde ao campo de direções dado.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
(j)
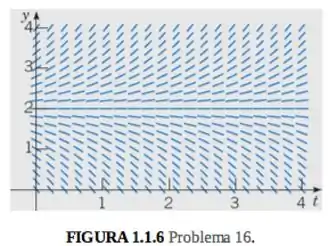
Campo de direções na figura 1.1.6.
Passo 1
Campos de direções são ferramentas valiosas no estudo de soluções de equações diferenciais da forma
Em que é uma função dada de duas variáveis, , algumas vezes chamada de função taxa. Um campo de direções pode ser constuido calculando em cada ponto de uma malha retangular. Em cada ponto da malha desenha-se um pequeno segmento de reta cujo coeficiente angular é o valor da função naquele ponto.
Um campo de direções fornece uma boa ideia do comportamento global das soluções de uma equação diferencial.
Para construir campos de direções não precisamos resolver nossa EDO, basta calcular a função dada muitas vezes.
Passo 2
Podemos ver que para , o seguinte fato ocorre, há uma divergência de 2, além de que 2 é uma solução de equilíbrio, logo é uma solução de Visto isso, ficamos com as letras (c) e (j) , mas para , vemos que é positivo, de modo que a letra (c) é a correta.
Resposta
(c)