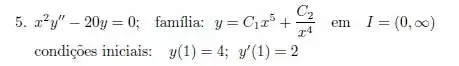Exercícios de Introdução à EDO - Lista de Exercícios Resolvida
Questão 1
Sabe-se que é uma família de soluções para no intervalo . Encontre um membro dessa família satisfazendo as condições iniciais e .
Ver solução completaQuestão 2
Considere a equação diferencial , com e funções reais.
Sabendo que e são soluções da equação determine e .
Ver solução completaQuestão 3
Problema 6 - Encontre valores de para que seja uma solução para cada equação diferencial.
(b)
Ver solução completaQuestão 4
Problema 6 - Encontre valores de para que seja uma solução para cada equação diferencial.
(a)
Ver solução completaQuestão 5
Problema 4 - Verifique que uma família a um parâmetro de soluções para
é . Determine um valor de para que seja uma solução singular para a equação diferencial.
Ver solução completaQuestão 6
Problema 7 - Mostre que e são ambas soluções para
As funções, e , com e constantes arbitrárias, são também soluções? A soma, é uma solução?
Ver solução completaQuestão 7
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(z) ; .
Ver solução completaQuestão 8
Problema 3 - Verifique se a função definida por partes é uma solução para a equação diferencial dada
(a) ;
Ver solução completaQuestão 9
Problema 3 - Verifique se a função definida por partes é uma solução para a equação diferencial dada.
(b) ;
Ver solução completaQuestão 10
Verifique se a função é solução da equação diferencial ordinária (EDO) dada
Ver solução completaQuestão 11
Verifique se a função é solução da equação diferencial ordinária (EDO) dada
Ver solução completaQuestão 13
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(o) .
Ver solução completaQuestão 14
Determine os possíveis valores da constante para que a função seja solução da equação , no intervalo .
Ver solução completaQuestão 15
Verifique se a função é solução da equação diferencial ordinária (EDO) dada
Ver solução completaQuestão 16
Verifique se a função é solução da equação diferencial ordinária (EDO) dada
Ver solução completaQuestão 17
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 18
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(g) .
Ver solução completaQuestão 19
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(l) .
Ver solução completaQuestão 20
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(n) .
Ver solução completaQuestão 21
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(t) .
Ver solução completaQuestão 22
Questão 2: Sabendo que é uma diferenciável que satisfaz a identidade
Para todo , podemos concluir que
- e .
- e .
- e .
- e .
- e não há informação suficiente para concluir quanto vale .
Questão 23
Verifique se a função é solução da equação diferencial ordinária (EDO) dada
Ver solução completaQuestão 24
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(f) .
Ver solução completaQuestão 25
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(a) .
Ver solução completaQuestão 26
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(k) .
Ver solução completaQuestão 27
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(b) .
Ver solução completaQuestão 28
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(c) .
Ver solução completaQuestão 29
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(h) .
Ver solução completaQuestão 30
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(d) .
Ver solução completaQuestão 31
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(e) .
Ver solução completaQuestão 32
Problema 1 - Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
j) .
Ver solução completaQuestão 33
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(w) .
Ver solução completaQuestão 34
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(p) .
Ver solução completaQuestão 35
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(r) .
Ver solução completaQuestão 36
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 37
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 38
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 39
3 - Determine a ordem da equação diferencial e diga se ela é linear ou não-linear.
e)
Ver solução completaQuestão 40
3 - Determine a ordem da equação diferencial e diga se ela é linear ou não-linear.
d)
Ver solução completaQuestão 41
3 - Determine a ordem da equação diferencial e diga se ela é linear ou não-linear.
b)
Ver solução completaQuestão 42
"As equações diferenciais começaram com o estudo de cálculo por Isaac Newton (1642-1727) e Gottfried Wilheim Leibnitz (1646-1716), no século XVII." Boyce e Di Prima.
Com relação às equações diferenciais é SOMENTE correto afirmar que
- Chama-se equação diferencial toda equação em que figura pelo menos uma derivada ou diferencial da função incógnita.
- Chama-se ordem de uma equação diferencial a ordem da derivada de mais alta ordem da função incógnita que figura na equação.
- Chama-se grau de uma equação diferencial o maior expoente da derivada de mais alta ordem da função incógnita que figura na equação.
( )
( )
( )
( )
( )
Ver solução completaQuestão 44
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(y) .
Ver solução completaQuestão 45
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 46
Responda falso ou verdadeira justificando a sua resposta, ou seja, prove se for verdadeiro ou dê um contra exemplo se for falso:
Se é uma solução particular de uma EDO linear de primeira ordem então a função também é solução.
Ver solução completaQuestão 47
Problema 5 - Verifique que uma família a um parâmetro de soluções para
é . Mostre que a relação define uma solução singular para a equação no intervalo .
Ver solução completaQuestão 48
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(j) .
Ver solução completaQuestão 49
3 - Determine a ordem da equação diferencial e diga se ela é linear ou não-linear.
f)
Ver solução completaQuestão 50
3 - Determine a ordem da equação diferencial e diga se ela é linear ou não-linear.
a)
Ver solução completaQuestão 51
3 - Determine a ordem da equação diferencial e diga se ela é linear ou não-linear.
c)
Ver solução completaQuestão 52
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(x) .
Ver solução completaQuestão 53
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(q) .
Ver solução completaQuestão 54
Determine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaQuestão 55
Determine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaQuestão 56
Determine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaQuestão 57
Determine a ordem das equações a seguir. Classifique-as em lineares ou não lineares e especifique se cada equação linear é ou não homogênea.
;
Ver solução completaQuestão 58
Dadas as EDOs abaixo, determine quais são lineares.
I-
II-
III-
( ) Apenas a I
( ) Apenas a III
( ) Nenhuma alternatina anterior está correta
( ) Apenas a II.
( ) I, II e III são lineares.
Ver solução completaQuestão 59
Classificando as seguintes EDOs como LINEAR ou NÃO LINEAR
a)
b)
encontramos:
( ) (a) não linear (b) não linear
( ) impossível identificar
( ) (a) linear (b) não linear
( ) (a) linear (b) linear
( ) (a) não linear (b) linear
Ver solução completaQuestão 60
Questão 2: Sobre as soluções lineares, isto é, da forma , da equação podemos afirmar que:
- Há infinitas soluções lineares.
- Não há soluções lineares.
- Há uma única solução linear.
- Há um par de soluções lineares.
- Nenhuma das demais alternativas:
Questão 61
Verifique se a função é solução da equação diferencial ordinária (EDO) dada
Ver solução completaQuestão 62
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(s) .
Ver solução completaQuestão 63
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 64
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(i) .
Ver solução completaQuestão 65
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(m) .
Ver solução completaQuestão 66
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completaQuestão 67
Problema 2 - Verifique se a função dada é uma solução para a equação diferencial. ( e são constantes).
(v) .
Ver solução completaQuestão 68
Classifique as equações diferenciais dizendo se elas são lineares ou não-lineares. Dê também a ordem de cada equação.
Ver solução completa