Dado a circunferência de equação , ache a maior distância entre o ponto (4, 5) e um ponto na circunferência.
Passo 1
Poderíamos fazer essa questão da mesma forma que fizemos as outras dessa seção, encontrando a derivada e tudo mais, mas dá pra fazer e um jeito mais simples e geométrico. Vamos desenhar tudo e usar algumas propriedades da circunferência e distância entre pontos.
Passo 2
Vamos começar esboçando isso que a questão fala, uma coisa de cada vez. Essa circunferência que ele diz tem equação , isso é uma circunferência centrada na origem de raio :
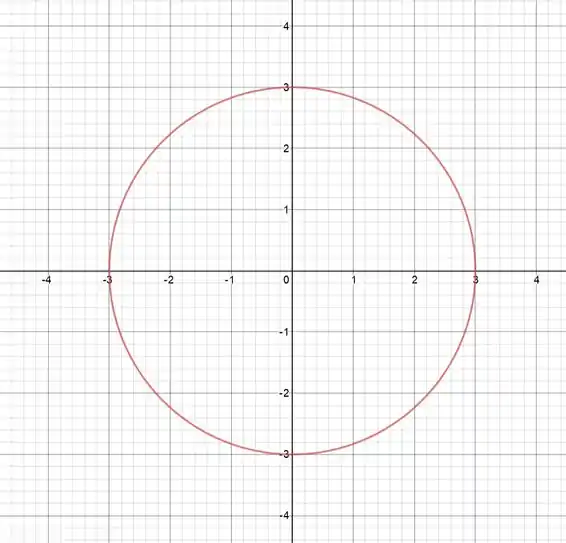
Agora vamos colocar o ponto nesse gráfico:
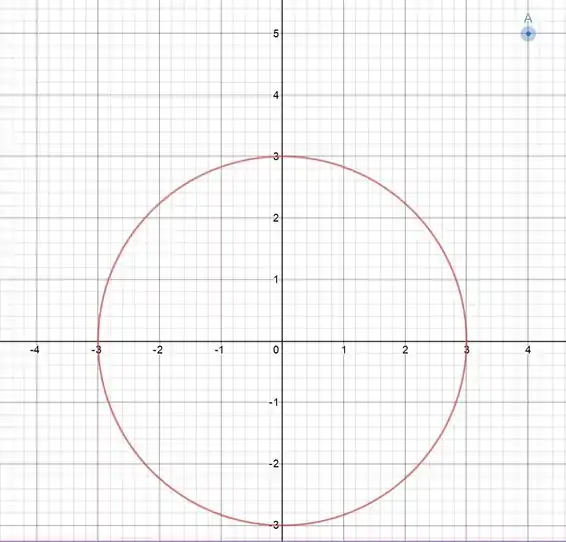
Passo 3
Queremos a maior distância entre a circunferência e o ponto, então vamos ficar com uma reta que liga o ponto ao raio da circunferência lá do outro lado:
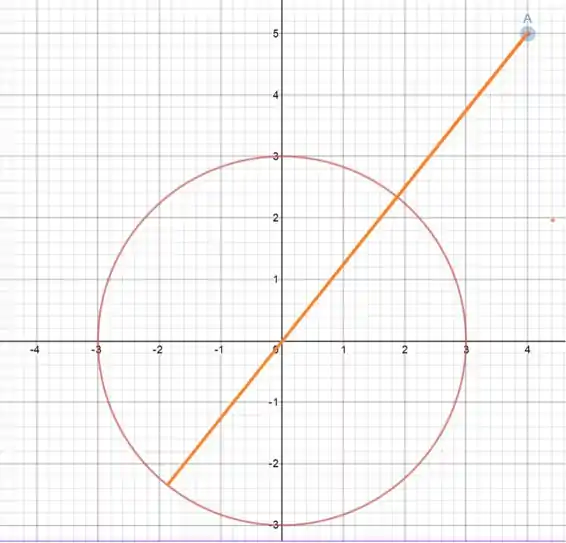
Se encontrarmos o tamanho do pedaço do segmento de reta laranja que está fora da circunferência; e somarmos a ele o diâmetro da circunferência teremos o tamanho que queremos!
A distância desse ponto até o centro da circunferência será:
E como:
Agora vamos somar a e teremos a distância que queremos.
Não tem pra que complicar a questão e sair procurando derivada, lembre-se que a geometria é uma grande amiga do estudante!
Resposta
unidades.